© h.hofstede (h.hofstede@hogeland.nl)

Frequentietabellen vergelijken
       
Laten we net als in de vorige les gewoon eens twee frequentieverdelingen nemen en die proberen met elkaar te vergelijken.
Hieronder staan de tijden die twee scholen van 120 leerlingen hebben gelopen op de 100 meter, ingedeeld in klassen.
       
tijd frequentie
klas A		 frequentie
klas B
10.5-11.0
11.0-11.5
11.5-12.0
12.0-12.5
12.5-13.0
13.0-13.5
13.5-14.0
14.0-14.5
14.5-15.0
15.0-15.5
15.5-16.0		 1
5
8
13
17
18
21
14
10
8
5		 0
0
2
8
26
29
34
10
7
3
1
       
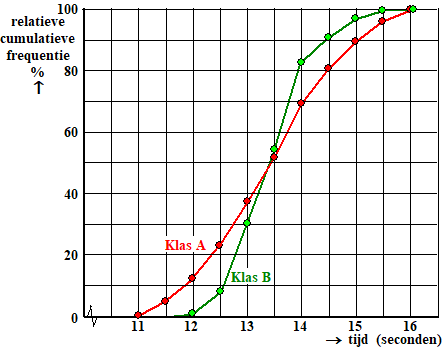
De vraag is:  hoeveel verschillen deze frequentieverdelingen?
Als je alleen het gemiddelde uitrekent dan vind je voor klas A  13,43  en voor klas B óók.  Dat zegt dus niets.
Toch zijn er natuurlijk wel verschillen. We zullen dus andere manieren moeten vinden om die boven water te halen.

Cumulatieve Frequentiepolygoon.

Als je van deze twee verdelingen in één figuur een cumulatieve frequentiepolygoon maakt (deze les) dan krijg je zoiets:
       

       
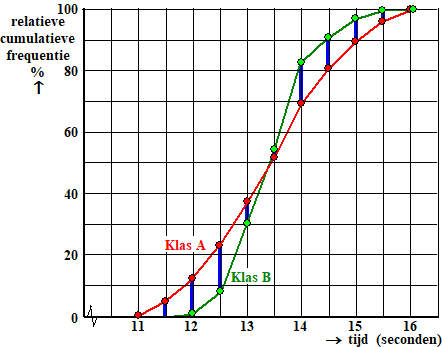
Je ziet dat er ondanks hetzelfde gemiddelde wel degelijk verschillen zijn, want die beide figuren lopen op een aantal plaatsen aardig uit elkaar.
We spreken daarom af dat we als maat voor het verschil de maximale verticale afstand tussen beide grafieken nemen. Dat is dus het grootste verschil in cumulatieve frequenties dat voorkomt, dus het langste blauwe lijntje hieronder:
       

       
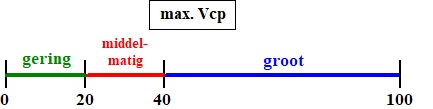
't Is natuurlijk handiger om dat af te lezen uit een tabel en niet uit een figuur. Het grootste verschil is 14,2% en is bij de klasse 12.0-12.5. Dit maximale verschil in cumulatieve percentage wordt ook wel afgekort max.Vcp genoemd. 

Is die 14,2 nou groot of klein?
We spreken het volgende als vuistregels af:
       

       
       
  OPGAVEN.
       
     
1. Examenopgave Havo, Wiskunde A, 2021-III

In de tabel hieronder zie je de resultaten van een enquête die door een middelbare school is gehouden onder de ouders. Je ziet de resultaten op de stelling "De schoolregels zijn duidelijk"  die in 2018 op die school door 700 leerlingen en 500 ouders beantwoord is.

       
 
stelling:  "De schoolregels zijn duidelijk"
  leerlingen ouders
zeer oneens 7 (1%) 10 (2%)
oneens 7 (1%) 15 (3%)
zowel eens als oneens 49 (7%) 60 (12%)
eens 343 (39%) 225 (45%)
zeer eens 294 (42%) 190 (38%)
       
  Met behulp van het formuleblad kun je nagaan dat het verschil tussen de leerlingen en de ouders bij deze stelling gering is. Als er meer ouders hadden gekozen voor ‘zowel eens als oneens’ in plaats van ‘eens’, dan zou het verschil tussen de leerlingen en de ouders groter zijn.
Bereken het minimale aantal ouders dat voor ‘zowel eens als oneens’ in plaats van ‘eens’ had moeten kiezen, zodat het verschil tussen de leerlingen en de ouders niet meer gering zou zijn, maar minstens middelmatig.
       
2. Het is voor websites als YouTube erg belangrijk dat kijkers lang genoeg naar een reclame kijken, en niet direct wegzappen. Immers: hoe langer men kijkt, des te meer inkomsten zal de adverteerder hebben dus des te meer adverteerders willen hun advertenties graag op YouTube zetten.
Hieronder zie je twee beelden uit filmpjes van de concurrerende make-up merken Rimmel London en Maxfactor.
       
 

       
 

Op internet kun je natuurlijk makkelijk bijhouden hoe lang men gemiddeld naar een filmpje kijkt.
Dat heeft men voor deze  twee reclamefilmpjes (van elk 60 seconden) gedaan en dat gaf de volgende tabel:
       
 

Kijktijd
(in seconden)

aantal bezoekers

Rimmel London

Maxfactor

0 - < 5

834

68

5 - < 10

821

156

10 - < 15

764

294

15 - < 20

732

481

20 - < 30

535

1430

30 - < 40

132

1412

40 - < 50

45

764

50 - 60

24

231

 

 

 

Totaal

3887

4836
       
  Bereken met MaxVcp of het verschil in kijktijd tussen deze twee filmpjes gering, middelmatig of groot is.
       
3.

Een aantal dagen is de gemiddelde dagtemperatuur gemeten in de steden Parijs en Kopenhagen.

Hieronder zie je van de resultaten daarvan in één figuur twee relatieve cumulatieve frequentiepolygonen.
       
 

       
  Eén van beiden hoort bij een normale verdeling.
       
  a. Leg duidelijk uit welk van beiden bij een normale verdeling hoort, en geef  ook aan hoe de verdeling van de andere wordt genoemd. 
       
  b. Bepaal het MaxVcp van deze verdelingen en leg daarmee uit of het verschil tussen de temperaturen in deze twee steden groot, middelmatig of klein is.
       
 
       

© h.hofstede (h.hofstede@hogeland.nl)