| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Boxplots vergelijken |
 |
Je kunt een boxplot handig gebruiken om iets duidelijker aan te geven of
er tussen twee metingen van verschillende groepen een (groot) verschil
zit of niet.
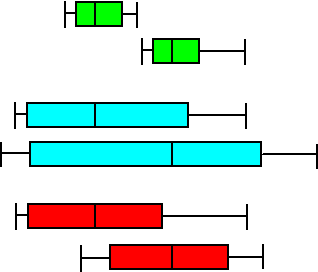
Hieronder zie je drie setjes (in drie kleuren) van twee boxplots. De
medianen van de drie bovenstens zijn gelijk en ook de medianen van de
drie ondersten. |
| |
|
|
|
|
 |
| |
|
|
|
Wat alleen de medianen betreft
zou je dus kunnen stellen dat de verschillen tussen de bovenste en de
onderste boxplots in alle drie de gevallen hetzelfde zijn.
Toch is dat duidelijk niet zo!
De groene twee verschillen eigenlijk heel veel: er zijn eigenlijk
helemaal geen gelijke metingen geweest, alles is verschillend. De
grootste van de ene is nog kleiner dan de kleinste van de tweede.
De blauwe twee verschillen erg weinig, de twee middelste blauwe boxen
zijn aardig vergelijkbaar, er overlappen veel metingen.
De roden zitten daar een beetje tussen in. Niet heel veel verschillend
zoals de groenen, ook niet erg weinig zoals de blauwen.
Maar ja, wat vinden we een "groot" verschil en wat een "klein". Kwestie
van smaak?
Je snapt wel dat een "kwestie van smaak" niet kan in de wiskunde. We
maken daarom (nog steeds vrij willekeurig) de volgende afspraak:
(daarbij bedoelen we met de "box" van een boxplot het deel tussen Q1 en
Q3: het eigenlijke doosje) |
| |
|
|
|
|
Het
verschil tussen twee boxplots: |
| de boxen overlappen helemaal niet. |
het verschil is groot |
| de boxen overlappen wel, en minstens één van beide
medianen
ligt buiten de box van de andere plot. |
het verschil is middelmatig |
| alle andere gevallen. |
het verschil is klein |
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
OPGAVEN. |
| |
|
|
|
| 1. |
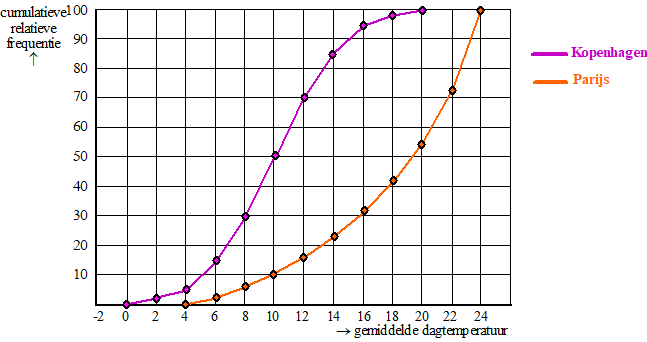
In de laatste opgave
van de vorige les bepaalden we met MaxVcp of het verschil in temperatuur
tussen Kopenhagen en Parijs groot, middelmatig of gering was.
Dat deden we aan de hand van de volgende twee cumulatieve
frequentiepolygonen: |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Bepaal met behulp van
boxplots opnieuw of het verschil groot, middelmatig of
gering is |
| |
|
|
|
| 2. |
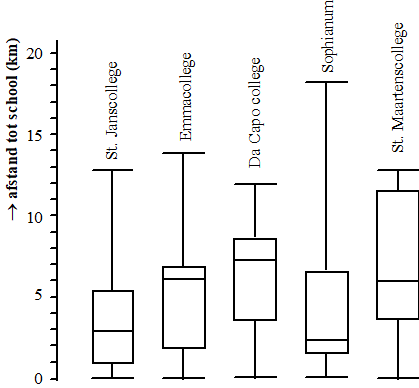
Voor 5 Limburgse
scholen is de gemiddelde afstand die leerlingen naar school moeten
afleggen bepaald.
Dat gaf de vijf boxplots hieronder. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
a. |
Welke school heeft de grootste spreidingsbreedte? Leg duidelijk
uit. |
| |
|
|
|
| |
b. |
Welke school heeft de grootste kwartielafstand? Leg duidelijk
uit |
| |
|
|
|
| |
c. |
Zijn er scholen waartussen het verschil wiskundig gezien
klein genoemd kan worden? Zo ja welke? Geef een
duidelijke uitleg. |
| |
|
|
|
| 3. |
De consumentenbond
heeft twee verschillende soorten 0.0 bier getest. Men vroeg een groot
aantal mensen om de merken Heineken 0.0 en Bavaria 0.0 te proeven
en er een cijfer op schaal 1 tot 10 aan te geven.
Dat leverde de volgende tabel op: |
| |
|
|
|
| |
| cijfer |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| aantal bij Heineken 0.0 |
20 |
34 |
56 |
62 |
75 |
80 |
54 |
60 |
47 |
12 |
| aantal bij Bavaria 0.0 |
5 |
20 |
22 |
45 |
68 |
83 |
91 |
72 |
52 |
22 |
|
| |
|
|
|
| |
Bepaal met behulp van
boxplots of het verschil tussen beide biermerken groot,
middelmatig of gering is. |
| |
|
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|