Nieuwe pagina 1

© h.hofstede (h.hofstede@hogeland.nl)

Redeneren met exponentiële formules.

In deze les hebben we al eerder bekeken hoe je aan de hand van formules kunt beredeneren of de grafiek ervan stijgt of daalt en of er grenswaarden zijn. Dart deden we toen met wortels, breuken en machten.
In deze les gaan we daar exponentiële formules aan toevoegen.

Daarvoor zijn vier eigenschappen van exponentiële formules belangrijk, en dat zijn:

als g groter dan 1 is, dan geldt:
1.	Als t groter wordt dan wordt g^t ook groter
2.	Als t een heel groot negatief getal wordt, dan wordt g^t gelijk aan nul.

als g kleiner dan 1 is dan geldt:
3.	Als t groter wordt, dan wordt g^t kleiner
4.	Als t een heel groot positief getal wordt, dan wordt g^t gelijk aan nul.

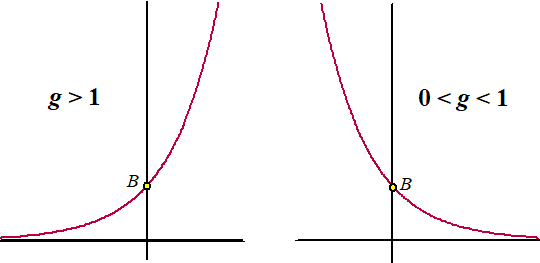
Het zit hem allemaal in die twee grafieken van g^x uit de vorige les.

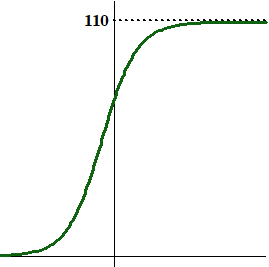
Een voorbeeldredenering.

Neem de volgende formule:

Als t groter wordt, dan wordt 0,8^t kleiner (regel 3, want 0,8 < 1)
Dan wordt 2 + 0,8^t ook kleiner
Dan wordt de hele breuk groter want de noemer wordt kleiner.
Dus N wordt groter, dus de grafiek stijgt.

Als t heeeeel erg groot positief wordt, dan wordt 0,8^t nul (regel 4)
Dan wordt de noemer ongeveer 2 + 0 = 2
Dan wordt de hele formule ²²⁰/₂ = 110
De grenswaarde aan de rechterkant is dus N = 110

Als t heeeeel erg groot negatief wordt dan wordt 0,8^theel erg groot,
Dan wordt de noemer heel erg groot.
Dan wordt de hele formule bijna nul.
De grenswaarde aan de linkerkant is N = 0.

Hiernaast zie je dat dat inderdaad allemaal klopt met de grafiek van N.

Als je het niet zeker weet....

Als je het niet meer zeker weet kun je natuurlijk altijd op je GR kijken wat er gebeurt.
Stelt dat je wilt weten wat 0,8^t in het voorbeeld hierboven wordt als t heel groot negatief wordt...
Dat toets je gewoon in 0,8^(-100) en dan zie je vanzelf dat dat een heel groot getal wordt (4909093465).

OPGAVEN.

Leerpsychologen zeggen dat het beter is om twee keer 1 kwartier ergens aan te leren dan één keer een half uur. In de formule hieronder is deze leerpsychologische wet terug te vinden.

E(t) = 100 – (100 – B)·0,7^t

Daarin is B het percentage van de stof dat je aan het begin al kent, en E het percentage dat je na t kwartier aan één stuk door leren kent (als je dus begint met B%)

Karin wil de stof uiteindelijk voor 80% kennen. Ze berekent met de formule hierboven dat ze dan nog 58 minuten moet leren. Voor hoeveel procent kent ze de stof nu al?

Leg met de formule duidelijk uit welke grenswaarde E heeft.

Leg met de formule duidelijk uit of de grafiek van E stijgt of daalt.

Een bioloog bestudeert de oppervlakte (in mm²) van een bacteriekolonie op een Petrischaal in zijn laboratorium. Na een groot aantal metingen stelt hij de volgende formule op:

met A de oppervlakte in mm² en t de tijd in dagen.

Leg met de formule duidelijk uit of de grafiek van A stijgt of daalt.

Hoe groot zal de oppervlakte uiteindelijk worden?

Om het korte-termijn geheugen van een persoon te testen heeft men de zogenaamde MEM-test ontworpen (Memory-Evaluation-Method).

Daarin laat men de proefpersoon een serie van 10 dia's te zien waarbij elke keer 2 plaatjes naast elkaar zichtbaar zijn.
Elke dia is daarbij 10 seconden zichtbaar.

Na afloop moet de proefpersoon zoveel mogelijk koppels noemen.
Als de persoon er minstens 8 goed heeft stopt de test.
Als de persoon er minder dan 8 goed heeft krijgt hij/zij dezelfde 10 dia's nogmaals te zien.

Men herhaalt de test net zolang totdat de proefpersoon minstens 8 plaatjes goed kan noemen.

Het aantal keer (A) dat de test uitgevoerd is bepaalt vervolgens de Geheugenscore G.
Dat gaat volgens de volgende tabel:

aantal A	1	2	3	4 - 5	6 - 7	8 - 9	10 - 11	12 - 15	16 - 20	>21
score G	10	9	8	7	6	5	4	3	2	1

Een formule die redelijk goed bij deze tabel past is G = 5 · 1,1⁸ - A

Laat zien dat voor A van 12 tot en met 15 deze formule inderdaad de juiste score G oplevert.

Beredeneer met de formule dat de score G stijgt als het benodigde aantal A kleiner wordt.

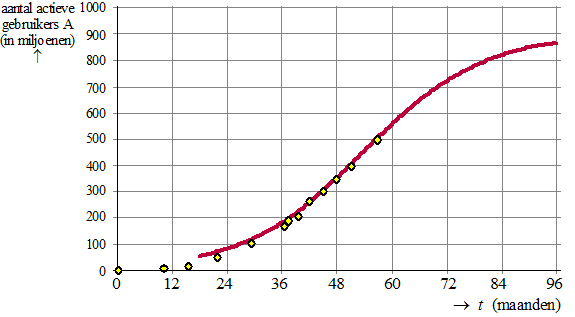
Examenvraagstuk HAVO wiskunde A, 2015 - I

Facebook is een sociaalnetwerksite, opgericht door Mark Zuckerberg in februari 2004. In het begin konden alleen studenten van Harvard College lid worden, later werden ook studenten van andere universiteiten toegelaten. In september 2006 werd Facebook geheel openbaar. Iedereen vanaf 13 jaar, waar ook ter wereld, kreeg de mogelijkheid om zich te registreren en actief gebruik te gaan maken van de site.

Het aantal actieve gebruikers steeg de eerste jaren spectaculair.

Het bleek erg optimistisch om aan te nemen dat de groei zich lineair voortzet. Al in 2011 voorspelden sommigen dat de groei verder zou afnemen. In de volgende figuur zie je een grafiek die bij deze voorspelling past.

Bij deze grafiek hoort de formule:

Hierin is A het aantal actieve gebruikers in miljoenen en t de tijd in maanden met t = 0 op 1 december 2005.

Bereken voor welke gehele waarde van t er volgens de formule voor het eerst meer dan 730 miljoen actieve gebruikers zijn.

Volgens de formule zal het aantal actieve gebruikers blijven stijgen, uiteindelijk nauwelijks meer toenemen en een grenswaarde benaderen.

Beredeneer aan de hand van de formule dat het aantal actieve gebruikers blijft stijgen

Bepaal de grenswaarde van de formule.