© h.hofstede (h.hofstede@hogeland.nl)

Stabiele Huwelijken.
       
Neem een groep mannen Y en een groep vrouwen X (laten we ze maar naar hun chromosomen noemen).  Neem verder aan dat iedere man en vrouw een voorkeurslijstje heeft voor degene van het andere geslacht waarmee hij of zij zou willen trouwen.
Een matching noemen we stabiel als er niet een Xi en een Yi te vinden zijn die beiden elkaar prefereren boven hun huidige partner. Immers dan zouden ze er met elkaar vandoor gaan.

Voorbeeld.
Stel we hebben  3 vrouwen en 3 mannen met de volgende voorkeurslijstjes:
       
 

       
Stel verder dat we de volgende matching hebben gemaakt:
 

X1 ⇔ Y3
X2 ⇔ Y1
X3 ⇔ Y2
       
Dan is dat geen stabiele matching. Y1 heeft liever X1 dan zijn huidige X2  en  X1 heeft ook liever Y1 dan haar huidige Y3
Kortom:  X1 en Y1 gaan er met elkaar vandoor en laten Y3 en X2 bedroefd achter.....
Toch zijn er met deze voorkeurslijstjes best stabiele matchings te maken. Meerdere zelfs. Hier zijn er twee:
       

X1 ⇔ Y1
X2 ⇔ Y2
X3 ⇔ Y3
 

X1 ⇔ Y2
X2 ⇔ Y3
X3 ⇔ Y1
       
Ga zelf maar na dat dit stabiel is. In de eerste wil bijvoorbeeld Y3 liever X1 dan zijn huidige X3,  maar X1 wil niet liever Y3 dan haar huidige Y1.
Het blijkt dat er, wat de voorkeuren ook zijn, altijd een stabiele matching te maken is! We zullen dat later gaan bewijzen, maar voor de verandering beginnen we eerst eens met een recept (algoritme) om zo'n stabiele matching te maken.
       
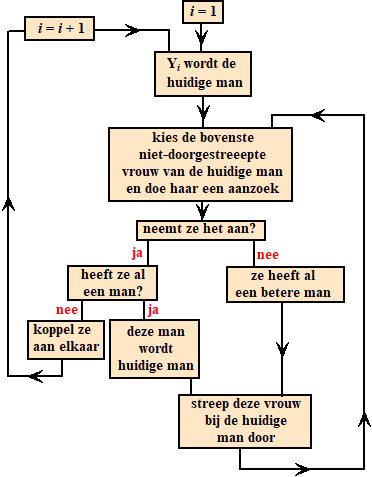
Een huwelijksalgoritme.

Zó maak je een stabiele situatie:
       

       
• Eindigt dit algoritme altijd?  Jazeker, want een man doet nooit bij dezelfde vrouw twee keer een aanzoek.
• Levert dit algoritme een matching op?  Jazeker, zodra een vrouw een partner heeft raakt ze nooit meer zonder partner (ze wisselt hem hoogstens in), en zolang er nog een man zonder partner is moet er ook nog een vrouw zonder partner zijn. Daar zal hij uiteindelijk een aanzoek aan doen, ook al is het de laatste op zijn lijstje.
• Levert het algoritme een stabiele matching?
Tja, dat is een lastiger vraag.....
Stel dat er nog een tweetal X1Y1 is, dat als partner een ander heeft, maar beiden liever elkaar zou hebben.
Stel de huidige paren zijn X1Yi en  XjY1 .
Y1 komt vóór Yi op de lijst van X1, dus op een bepaald moment moet X1 wel een aanzoek aan Y1  hebben gedaan, anders was hij nooit bij Yi terechtgekomen.
Maar dat aanzoek heeft X1 kennelijk afgewezen! De enige mogelijke reden is dat ze op dat moment al een betere partner dan Y1 had. Maar dan kan ze later nooit met Y1 eindigen omdat de partners van een vrouw alleen maar verbeteren.
Kortom, de matching moet wel stabiel zijn.
       
Nog twee oneerlijke eigenschappen.

1.  Geen man kan zich verbeteren in de gevonden matching.
Elke man krijgt de eerste vrouw op zijn lijst die niet is doorgestreept.
Stel dat het paar X1Y1 in de matching voorkomt,
Dan heeft Y1 alle andere vrouwen op zijn lijst die hoger stonden dan X1 kennelijk moeten doorstrepen.

Stel dat hij zo'n vrouw X2 moest doorstrepen.
Dat kan 2 dingen betekenen:
•  X2 was al 


2.  Geen vrouw kan zich verslechteren in de gevonden matching.
 
       
       

© h.hofstede (h.hofstede@hogeland.nl)