| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Misleiding ? |
 |
| |
|
|
|
We hebben intussen in
dit hoofdstuk een groot aantal berekeningen en figuren gezien waarmee we
gegevens kunnen weergeven. Maar als dat op zoveel verschillende manieren
kan, dan kun je natuurlijk ook wel de manier kiezen die het best past
bij jouw standpunt.
Er wordt wel eens beweerd dat je met statistiek alles aannemelijk kunt
maken wat je maar wilt!!! |
| |
|
|
|
|
 |
| |
|
|
|
1. Keuze uit absoluut of
relatief.
Ik zal het verhaal van de drie verkopers vertellen.......
Drie verkopers moeten één voor
één bij de directie komen voor een functioneringsgesprek. Er
gonzen geruchten dat er met het oog op de komende inkrimpingen
iemand ontslagen moet worden!
De drie verkopers zullen alle drie afgerekend worden op hun
verkoopcijfers over het afgelopen halve jaar.
Dat zijn trouwens de volgende cijfers: |
| |
|
|
|
| verkoopcijfers |
| |
jan |
feb |
mrt |
apr |
mei |
jun |
| verkoper 1 |
320 |
343 |
373 |
428 |
488 |
568 |
| verkoper 2 |
170 |
210 |
266 |
346 |
440 |
540 |
| verkoper 3 |
51 |
79 |
112 |
162 |
250 |
340 |
|
| |
|
|
|
Verkoper 1
Verkoper 1 ziet het gesprek vol vertrouwen tegemoet. Hij is
al jarenlang degene die het meest verkoopt. Verreweg.
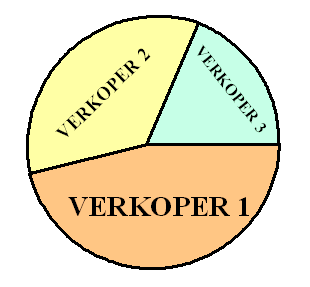
Om de directie straks nog eens extra te overtuigen maakt hij een
mooi cirkeldiagram waarin de totale verkopen van het afgelopen
half jaar zijn weergegeven.
(totale verkoop is 5486, zij verkochten resp. 2520 - 1972 - 994,
dus de middelpuntshoeken zijn afgerond 162º - 129º -
65º)
't Is wel duidelijk: verkoper 1 was duidelijk de beste
het afgelopen half jaar! |
 |
| |
Verkoper 2
Verkoper 2 ziet dat hij niet de grootste verkoop heeft, maar
zijn verkoop is in de loop van het halve jaar wel aan het
stijgen geweest. Hij besluit daarom de directie straks te
overtuigen met een mooi staafdiagram waarin van elke verkoper
staat hoe de toename en afname van zijn verkoop geweest is.
Dat wordt het volgende staafdiagram.
't Is wel duidelijk: verkoper 2 was duidelijk de beste het
afgelopen half jaar! |
| |
|
|
|
|
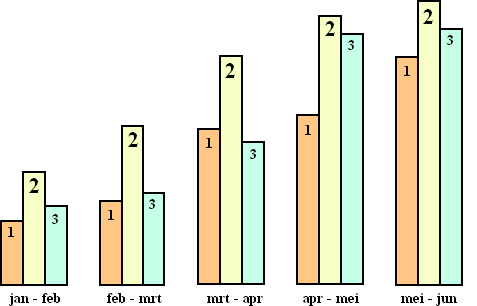 |
| |
|
|
|
Verkoper 3
Verkoper 3 is de Benjamin van de zaak. Hij is nog niet zo
lang in dienst, maar ziet toch dat zijn verkoopcijfers aardig
aan het stijgen zijn geweest.
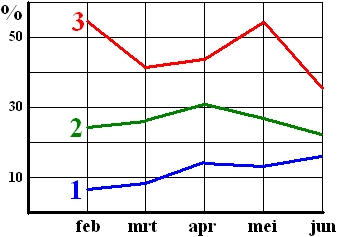
Zoals zo vaak wel een goede tactiek voor kleintjes is, besluit
hij over te stappen op de procenten.
Hij maakt in één figuur drie grafiekjes van de toename
van de
verkoopcijfers over de afgelopen maanden in procenten.
Die grafiekjes staan hiernaast.
't Is wel duidelijk: verkoper 3 was duidelijk de beste het
afgelopen half jaar! |
 |
| |
|
|
|
| En zo gaan alle
drie de verkopers dankzij de wiskunde vol vertrouwen hun gesprek
met de directie tegemoet !!! |
| |
|
|
|
|
2. Procenten van procenten. |
|
 |
| |
|
|
|
Een groot drugonderzoek,
beschreven door Lynn Parker in haar boek The Disease Mongers, testte
de drug cholestyramine op een groep van 3806 mannen. Men wilde kijken of
cholestyramine het cholesterolgehalte verlaagde, en dus hartaanvallen
verminderde.
1906 mannen kregen gedurende 10 jaar de drug, en een
controlegroep van 1900 niet.
In de eerste groep overleden in die 10 jaar 30 mannen aan een
hartaanval, in de controlegroep 38 mannen.
Dat scheelt niet zoveel; 8 mannen verschil van in totaal 3806 mannen.
Niet noemenswaardig zou je zeggen.
0,2%?
Maar nee! Laten we eerst procenten nemen. In de eerste groep
overleed 1,6% en in de controlegroep 2,0%.
Kijk; "Now we're getting somewhere!" Dat is een verschil van
0,4%. Dus vergeleken met 2,0% is die 1,6% een verlaging van 0,4/2
• 100 = 20%.
En zo hebben we toch weer een krantenkop:
|
| |
|
|
|
|
Wetenschappelijk
onderzoek wijst uit:
Cholestyramine verlaagt kans op hartinfarct met 20%! |
|
| |
|
|
|
|
Ik zou het morgen gaan kopen! Die 20% klinkt geweldig! Alhoewel;
een dokter die patiënten ermee behandelt zal bij ongeveer 1 op de 250
resultaat mogen verwachten. Maar ja, deze kop is minder mooi natuurlijk:
|
Wetenschappelijk
onderzoek wijst uit:
Cholestyramine helpt in 1 op de 250 gevallen! |
|
| |
|
|
|
3. Schaalverdelingen
manipuleren.
Door handig met de schaalverdeling van je grafieken te rommelen kun je
met slimme grafiekjes suggesties geven die er feitelijk niet of haast
niet zijn.
Deze soort "misbruik van de statistiek" komen we elke dag tegen!
Elke dag?
Ja, elke dag!!!Tenminste als je de krant leest.
Daar staan op de financiële pagina's altijd mooie grafiekjes om aan te
geven hoe het met de beursindexcijfers gegaan is.
Vandaag nu ik dit schrijf is het 30 juli 2004. Wacht maar even, dan loop ik naar beneden
om de krant te halen...... |
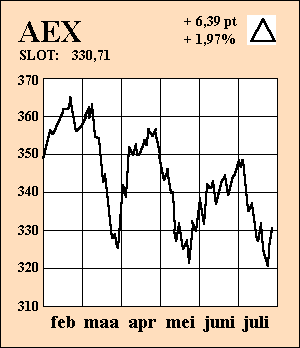
Zo daar ben ik alweer. Even
kijken... Ja hier bijvoorbeeld. Het grafiekje hiernaast uit de
Volkskrant geeft het verloop van de AEX-index weer.
Het lijkt op het eerste gezicht dit jaar stormachtig te verlopen met de
AEX. Toppen en dalen wisselen elkaar af.
Totdat je je realiseert dat de schaalverdeling op de verticale as niet
bij nul begint, maar bij 310 (de zaagtand die er dan hoort te staan is voor het gemak
maar weggelaten).
Ja hoor! Zo kan ik ook nieuws uit het niets fabriceren. In maart heeft
vast in de krant een verontrustend artikel over de sterke daling van de
beursindex gestaan, natuurlijk direct verbonden met een verontrustend
verhaal over de economie in het algemeen.
|
 |
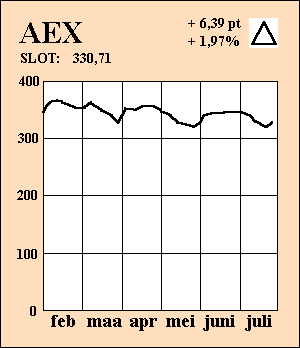
Maar als je de schaalverdeling wél
correct weergeeft dan krijg je iets als hiernaast.
Nogal een verschil met de vorige figuur!
Van de woeste schuimkoppen van de index is nog slechts een "rustig
kabbelend beekje" overgebleven!
Die spectaculaire daling in maart met dat verontrustende artikel, daar
blijft zo eigenlijk niets meer van over.
Maar ja, dan heb je als krant geen nieuws te melden....... |
 |
| |
|
|
|
| |
|
|
|
OPGAVEN. |
| |
|
|
|
| 1. |
In 1982 begon in Amerika een
grote "Cancer Prevention Study" waaraan bijna een miljoen
Amerikanen deelnamen. Na uitgebreide bestudering van de vragenlijsten
concludeerde "wetenschapper" Eric Jacobs van de
Amerikaanse kankervereniging in Atlanta:
Vitamine-E
supplementen verminderen het risico op blaaskanker.
Risico op overlijden vermindert met 40%! |
Luid gejuich van de vitaminesupplement fabrikanten natuurlijk.
Maar....... 40% van wát?
Het bleek dat Jacobs alleen verschil zag bij mensen die al 10
jaar of meer om de dag pillen gebruiken.
Van de 842565 niet-gebruikers stierven er in 10 jaar 1116 aan
blaaskanker.
Van de 21699 intensieve gebruikers stierven er in 10 jaar 24. |
| |
|
|
|
| |
a. |
Hoeveel procent van
de niet-gebruikers en hoeveel procent van de intensieve gebruikers
stierven er aan blaaskanker? |
| |
|
|
|
| |
b. |
Leg uit hoe Eric Jacobs aan die
40% kwam. |
| |
|
|
|
| |
c. |
Als 2000 mensen zich hier iets van zouden aantrekken en voortaan bijna
dagelijks vitamine-E bij zouden slikken, hoeveel minder doden zal dat
dan in 10 jaar opleveren? |
| |
|
|
|
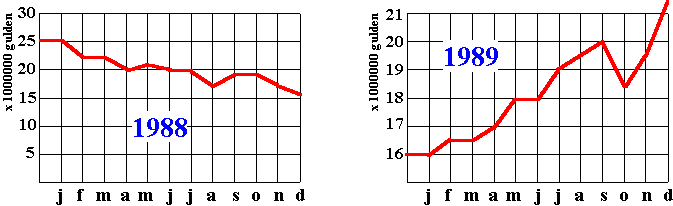
| 2. |
Hieronder staan twee grafiekjes uit een jaarverslag van een
grote onderneming. Zij geven de winst over de jaren 1988 en 1989 weer.
In het jaarverslag van 1988 was te lezen dat er sprake was van een "licht
dalende tendens". En in het verslag van 1989 is te lezen dat er
dat jaar een "spectaculaire winststijging" te zien was. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Leg duidelijk uit hoe
hier oplichterij is toegepast. |
| |
|
|
|
| 3. |
In een Zweedse krant stond de volgende
advertentie, van een soort Veilig-Verkeer-Organisatie: |
| |
|
|
|
| |
|
In het
afgelopen jaar verdronken 40
mensen bij
bootongelukken
Slechts VIJF van hen droegen een zwemvest!
DRAAG ALTIJD EEN
ZWEMVEST op een
boot!!!! |
|
| |
|
|
|
| |
Lijkt overtuigend nietwaar? En toch mist
hier een belangrijk, zeg maar gerust essentieel, gegeven.
Er staat namelijk niet bij hoeveel procent van alle mensen op een boot een zwemvest droegen, en
dat aantal is niet erg groot.
Stel bijvoorbeeld dat 5% van de mensen een zwemvest droegen.....
Kies een willekeurige groep van 5000 mensen op een boot, en neem aan dat
de gegevens uit de advertentie op hen van toepassing waren. |
| |
|
|
|
| |
a. |
Bereken hoeveel
procent van de zwemvestdragers verongelukten en hoeveel procent van de
niet-zwemvestdragers? |
| |
|
|
|
| |
b. |
Wat had de conclusie
van deze gegevens in dat geval moeten zijn? |
| |
|
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|