© h.hofstede (h.hofstede@hogeland.nl)

Soorten verdelingen
       
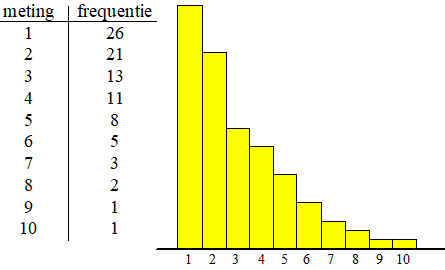
We hebben al eerder gezien dat je een serie waarnemingen of metingen kunt noteren in een frequentietabel en dat je er bijvoorbeeld een histogram van kunt maken.
Zo'n tabel of histogram noemen we in het algemeen een verdeling.

Hieronder zie je een paar soorten verdelingen (ze worden meestal als histogrammen getekend):
       

       
Een paar eigenschappen:
•  Bedenk dat de frequenties op de y-as staan en de gemeten waarden op de x-as.
•  "Rechtsscheef" en "Linksscheef" heten naar de kant waar ze de "staart" hebben zitten.
•  Bij relatieve frequenties is de totale oppervlakte 100%
•  De totale breedte heet ook wel de spreidingsbreedte.
•  De modus is de x-plaats van de top (bij meer toppen is er geen modus)
•  De kwartielafstand is de horizontale breedte van de middelste 75% van het histogram.
 

Mediaan en Gemiddelde.

De mediaan en het gemiddelde zijn iets lastiger uit zo'n verdeling af te lezen.
Ik zal het voordoen met de tabel en het histogram hieronder.
 


1. Mediaan.

De mediaan is gewoon het middelste getal van al je metingen, als je ze van klein naar groot hebt gezet. Omdat in een histogram elke waarneming als een blokje is aangegeven is het gewoon het middelste blokje van al die blokjes. Die blokjes zie je hieronder links.
Dat betekent dat de mediaan het getal op de x-as is, waarvoor geldt dat de oppervlaktes onder het histogram aan beide kanten precies gelijk zijn. Dat zie je in de rechterfiguur hieronder. De oranje oppervlakte is gelijk aan de groene oppervlakte.
De mediaan is 2 (bij de rode pijl)
       

       
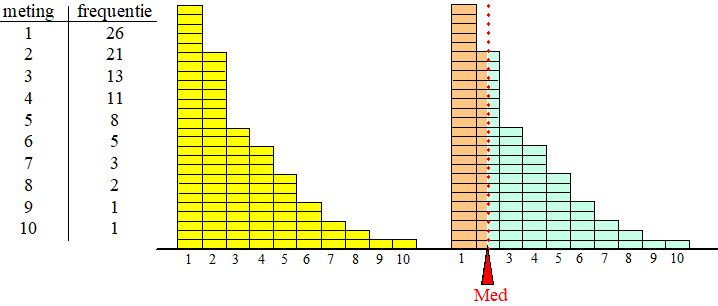
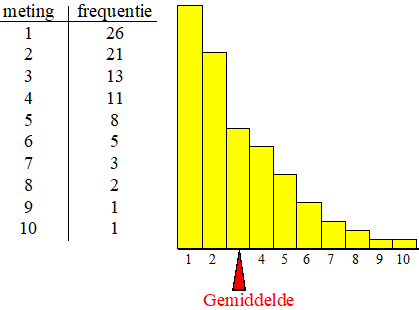
2.  Gemiddelde.

Voor het gemiddelde telt niet alleen het aantal blokjes mee, maar ook hoe ver ze op de x-as naar rechts liggen. De blokjes naar rechts tellen zwaarder mee, want dat stellen grotere getallen voor.
Om de plaats van het gemiddelde te vinden moet je je voorstellen alsof je het histogram op een plankje hebt staan dat je moet balanceren. Ongeveer zoiets:
       

       
Die pijl bij het gemiddelde is de plaats waarop het histogram "in evenwicht" is.

Je ziet dat bij een rechtsscheve verdeling het gemiddelde verder naar rechts ligt dan de mediaan.  Dat komt omdat die kleine blokjes aan de rechterkant zwaarder meetellen omdat ze grotere getallen voorstellen.
Je snapt dat bij een symmetrische verdeling het gemiddelde gelijk zal zijn aan de mediaan.
       

Bij een linksscheve- of rechtsscheve verdeling ligt het gemiddelde verder naar buiten dan de mediaan
       
Uitschieters.
       
Een uitschieter is een meetwaarde die ver naast de anderen meetwaarden ligt. Vaak zover zelfs dat we vermoeden dat we te maken hebben met een meetfout. Dat is wel vervelend want zulke hele kleine of hele grote meetwaarden hebben een behoorlijke invloed op het gemiddelde,
We laten ze daarom liever weg.

Hoeveel moet een meting afwijken om als uitschieter gezien te worden?

Meestal wordt het volgende principe gehanteerd:
       
 

"Een uitschieter ligt meer dan 1,5 keer de kwartielafstand onder Q1 of boven Q3"
       
Daarbij waren Q1 en Q3 het eerste kwartiel en het derde kwartiel (uit deze les)
In een plaatje:
       

       
Je ziet dat die uitschieters inderdaad behoorlijk ver naast de rest van de meetwaarden liggen.
Vaak worden zulke uitschieters niet meegenomen in de berekeningen, maar wel als losse stippen naast de boxplot getekend.
Dan zou een boxplot er zó uit kunnen zien:
       

       
Links is er één uitschieter, rechts zijn er twee.

Voorbeeldberekening.

Stel dat een serie meerwaarden hebt met  Q1 = 156  en   Q3 =  184.
Waar liggen dan eventuele uitschieters?

Q3 - Q1 = 28
28 • 1,5 = 42
156 - 42 = 104  en   184 + 42 = 226
Uitschieters zijn kleiner dan 104 of groter dan 226
       
Een mooi artikel over scheve verdelingen en toepassingen in de geneeskunde kun je vinden op:
 
       
 
       
                                       
       
  OPGAVEN.
       
1. Hieronder zie je een frequentieverdeling.
       
 
meting 2 3 4 5 6 7 8 9 10 11 12 13 14 15
aantal 1 3 4 4 5 7 7 9 10 12 14 15 16 12
       
  a. Bedenk zonder berekeningen of tekeningen te maken of deze verdeling rechtsscheef of linksscheef of symmetrisch is.
       
  b. Bereken de mediaan en het gemiddelde en controleer of die waarden kloppen met je antwoord op vraag a.
       
2. a. Een frequentieverdeling heeft  eerste kwartiel 145, tweede kwartiel 156 en derde kwartiel 172.
Geef aan welke metingen als uitschieters gezien mogen worden.
       
  b. Een frequentie verdeling heeft derde kwartiel  512.
Metingen boven 638 mogen als uitschieters worden gezien.
Bereken het eerste kwartiel.
       
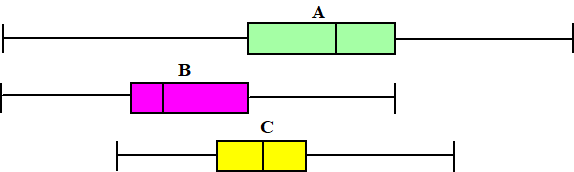
3. Hieronder zijn drie boxplots getekend van alle metingen, dus zonder rekening te houden met uitschieters.
Leg uit bij welke boxplot en aan welke kant (links of rechts) er sprake is van uitschieters.
       
 

       
4. Schets de vorm van een cumulatief frequentiepolygoon van een rechtsscheve verdeling.
       
       
 

© h.hofstede (h.hofstede@hogeland.nl)