© h.hofstede (h.hofstede@hogeland.nl)

Correlatie & Regressie met Excel.
       
Soms heb je te maken met twee variabelen en ben je benieuwd of er misschien een verband tussen die twee bestaat. Bijvoorbeeld of, als de ene groter wordt, de andere dat ook doet.

Dat kun je met Excel onderzoeken.

We doen dat met een  klein voorbeeld:  De cijfers die een groep van 10 leerlingen hebben gehaald op hun proefwerk Wiskunde en op hun proefwerk Natuurkunde.
Dat zijn deze cijfers:
       

leerlingnummer.

1

2

3

4

5

6

7

8

9

10

cijfer wiskunde.

8,2

4,9

5,4

6,9

3,3

7,9

8,8

4,5

5,8

7,9

cijfer natuurkunde.

8,4

3,8

7,9

8,0

5,0

6,9

7,2

5,8

4,6

5,8
 
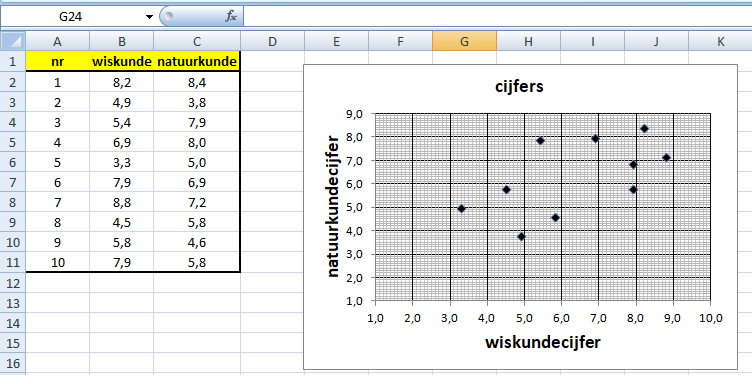
Laten we eerst in Excel een spreidingsdiagram maken, waarbij de wiskundecijfers op de x-as staan en de natuurkundecijfers op de y-as:
       

       
Je ziet in het spreidingsdiagram een beetje een soort van stijgende lijn. Dat zou betekenen dat een hoger wiskundecijfer "een beetje"  hoort bij ook een hoger natuurkundecijfer.  Er is een "soort van" verband tussen de cijfers.
       
Correlatiecoëfficiënt.
       
Gelukkig kan Excel voor ons bepalen hoe goed het verband tussen beide variabelen is, door een getal r  te berekenen dat de correlatiecoëfficiënt heet.
Dat getal r varieert van -1 tot 1, en het betekent:
       
r = -1 de punten liggen perfect op een dalende lijn.
r = 0 de punten liggen willekeurig door elkaar, er is geen verband.
r = 1 de punten liggen perfect op een stijgende lijn.
       
Hoe dichter r bij 1 of -1 ligt, des te sterker is het verband  (de "correlatie") tussen de twee variabelen.
Dus r = 0,9  betekent een sterkere correlatie (stijgend)  dan r = 0,8.
En r = -0,5 betekent een zwakkere correlatie (dalend)  dan r = -0,7

Je (of eigenlijk Excel natuurlijk) berekent r als volgt:
       

•

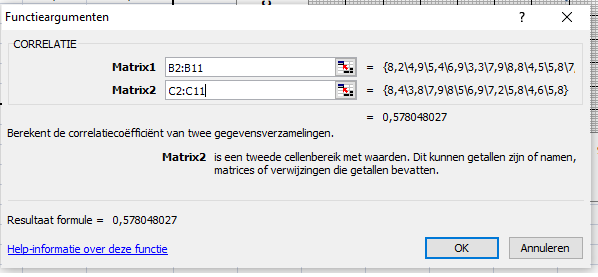
Kies achtereenvolgens:      Formules →  Meer functies → Statistisch → Correlatie
       

•

 Voer nu bij matrix1 de cellen van de x-variabele in  (in ons geval B2:B11) en bij matrix2 de cellen van de y-variabele (in ons geval C2:C11)
       

•

  Druk op OK en je vindt de correlatiecoëfficiënt  r = 0,578...

Dat betekent dat er een beetje een stijgende lijn is tussen x en y  (want r is positief), maar niet super goed, want r is niet dicht bij 1. Een beetje een licht stijgend effect tussen beide variabelen dus.

Het kan overigens ook in één keer door in de cel de formule    =correlatie(B2 : B11 ; C2 : C11) in te voeren (dubbele-punt tussen de cellen, punt-komma tussen de twee matrices)
       

Regressielijn.
       
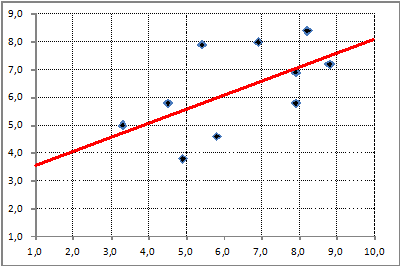
Excel kan zelfs voor ons berekenen welke rechte lijn het best past bij onze meetpunten. Die lijn heet de regressielijn, en de a en b daarvan (jeweetwel, die van  y = ax + b)   bereken je als volgt (merk op dat je de cellen op dezelfde manier invult als hierboven, eerst de y, dan de x):
       

a = index(lijnsch(C2:C11; B2:B11);1)
b = index(lijnsch(C2:C11; B2:B11);2)

       
Probeer het maar:  dat geeft a  = 0,4942...  en  b = 3,1966...

De beste lijn bij deze meetpunten is dus de lijn  y = 0,4842x + 3,1966

Kijk maar, lijkt aardig te kloppen toch?
       

       
 
 
  OPGAVEN
       
1. De volgende tabel geeft voor zeven dagen de hoogst gemeten temperatuur (T in ºC) op die dag en het aantal uren (u) zon.
       
 
T (in ºC) 16 17 17 18 19 20 22
u (in uren) 9 10 11 10 12 11 13
       
  a. Bereken de correlatiecoëfficiënt van deze gegevens.
       
  b. Je kunt de temperatuur ook uitdrukken in graden Fahrenheit. Daarvoor geldt: F = C • 1,8 + 32
(F = graden Fahrenheit, C = graden Celsius)
Verander de temperaturen naar graden Fahrenheit, en laat zien dat r hetzelfde blijft.
       

© h.hofstede (h.hofstede@hogeland.nl)