| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Betrouwbaarheidsintervallen |
 |
| |
|
|
|
We gaan in deze les
bekijken in hoeverre resultaten van een steekproef iets zeggen over de
populatie.
Laat één ding vooraf volkomen duidelijk zijn, misschien wel HET principe
van deze les: |
| |
|
|
|
|
We kunnen nooit met
volledige zekerheid iets beweren! |
|
| |
|
|
|
Stel dat je in een
(verantwoord) onderzoek hebt gevonden dat het gemiddelde gewicht van
zesjarige kinderen in een steekproef die je hebt gehouden gelijk is aan
23 kg (met een standaardafwijking van 6 kg). Dan lijkt het een redelijke
veronderstelling om te zeggen dat van alle kinderen in Nederland het
gemiddelde gewicht gelijk zal zijn aan ongeveer 23 kg. Hoe groter je
steekproef, hoe betrouwbaarder dat getal zal zijn.
Maar je weet het nooit helemaal zeker!
Overschrijdingskans.
Je vermoedt dat het gemiddelde gewicht voor heel Nederland ongeveer
gelijk zal zijn aan G ≈ 23 met een standaardafwijking van 6 kg.
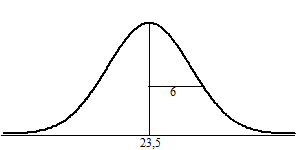
Maar als dat niet zo is, en G is bijvoorbeeld 23,5 kg met een
standaarddeviatie van 6 kg, dan ziet de gewichtsverdeling er in
werkelijkheid zóiets uit: |
| |
|
|
|
|
 |
| |
|
|
|
Ook dan zou jouw
steekproef dus best een waarde van 23 kunnen opleveren. Of zelfs nog
lager. Dat is natuurlijk wel een afwijking van de 23,5 maar niet een al
te grote. Geef toe: Het zou zelfs heel toevallig zijn als jouw
steekproef PRECIES 23,5 zou opleveren! Kortom: een afwijking zal
vaak voorkomen, maar een al te grote afwijking niet.
Betrouwbaarheidsinterval.
Bij het maken van een schatting voor een gemiddelde in een populatie
gaan we voortaan gebruik maken van het begrip "betrouwbaarheid".
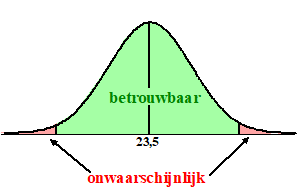
Stel dat we kiezen voor een betrouwbaarheid van 95%. Dan noemen we
de metingen die in een gebied van 95% rond het midden liggen
"betrouwbaar". De buitenste 5% van de klokvorm noemen we
"onwaarschijnlijk".
De metingen in het groene gebied hieronder zijn dus "betrouwbaar" en de
metingen in het rode gebied zijn "onwaarschijnlijk". |
| |
|
|
|
|
 |
| |
|
|
|
Terug naar ons probleem.
Wat was het probleem
ook al weer? Nou, stel dat we in een steekproef een gemiddelde van 23
hebben gemeten, wat kunnen we dan over het gemiddelde van de hele
populatie zeggen?
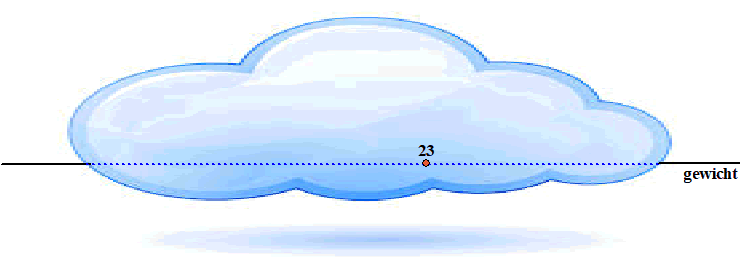
Ofwel: ergens in deze mist ligt een klokvorm verscholen, en wij
hebben als enige gegeven een gemeten gemiddelde van 23 (de rode stip). |
| |
|
|
|
 |
| |
|
|
|
Waar oh waar ligt het
gemiddelde van de werkelijke klokvorm........?????
Laten we ezeltje prik
gaan spelen..... |
| |
|
|
|
|
 |
| |
|
|
|
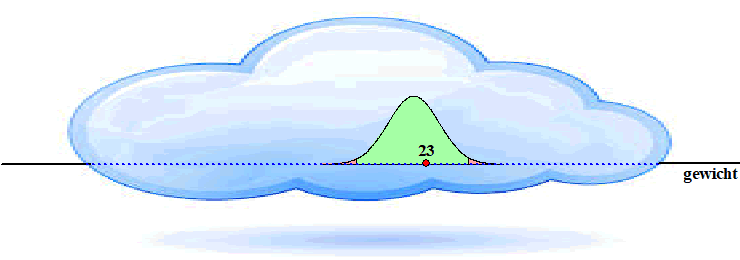
Jij moet de klokvorm hiernaast ergens op die getallenlijn
in die mist neerleggen,
waarbij de enige voorwaarde is dat onze meting van 23 kg een betrouwbare
meting moet zijn.
Bijvoorbeeld zó: |
 |
|
 |
| |
|
|
|
Het werkelijke
gemiddelde lijkt nu iets links van 23 te liggen, maar 23 is een
betrouwbare meting want ligt in het groene gebied van deze klokvorm..
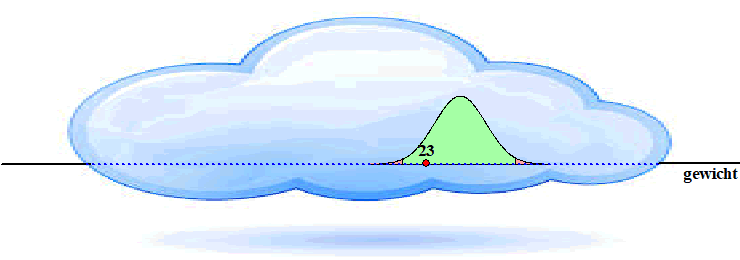
Of zó: |
|
 |
| |
|
|
|
Nu ligt het
werkelijke gemiddelde een stuk rechts van 23, maar 23 is nog steeds een
betrouwbare meting.
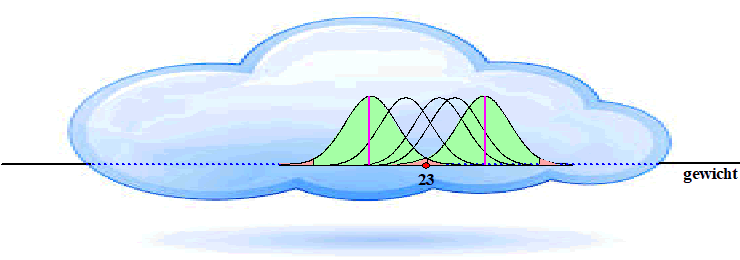
OK, geen kinderspelletjes neer; laten we direct aangeven wat de
uiterste grenzen voor het gemiddelde van de werkelijke klokvorm kunnen
zijn: |
| |
|
|
|
|
 |
| |
|
|
|
Alle gemiddeldes
tussen die twee paarse strepen zijn mogelijk als onze meting een
betrouwbare meting is.
Dat gebied waarin het werkelijke gemiddelde kan liggen noemen we het
95%-betrouwbaarheidsinterval. |
| |
|
|
|
|
Het 95%-betrouwbaarheidsinterval bij
een normale verdeling is
[x
- 2σ,
x
+ 2σ] |
|
| |
|
|
|
De standaardafwijking.
Als je het gemiddelde van een groot aantal (n) metingen neemt dan
is de variatie in zo'n gemiddelde veel kleiner dan de variatie in de
afzonderlijke metingen. Dat betekent dat de standaardafwijking van zo'n
gemiddelde kleiner wordt naarmate je steekproef groter wordt. Je gemeten
gemiddelde wordt betrouwbaarder als de steekproef groter is.
Het blijkt dat de standaardafwijking van zo'n gemiddelde gelijk is aan σ/√n waarbij
σ de gemeten standaarddeviatie van onze steekproef van
de afzonderlijke n
metingen is.
De regel voor het betrouwbaarheidsinterval moet daarom veranderd worden in: |
| |
|
|
|
|
Als een steekproef van n
metingen een gemiddelde
x
en een standaarddeviatie
σ oplevert,
dan is het 95%-betrouwbaarheidsinterval gelijk aan [x
- 2 • σ/√n ,
x
+ 2 • σ/√n] |
|
| |
|
|
|
Voorbeeld
Een antropoloog meet de lengtes van een steekproef van 100 vrouwen uit
een zekere populatie en vindt een gemiddelde van 179 cm met een
standaarddeviatie van 18 cm.
Wat kan hij concluderen over de hele populatie?
Oplossing.:
Voor een gemiddelde van 100 vrouwen geldt dan σ = 18/√100 = 1,8
179 + 2 • 1,8 = 182,6 en 179 - 2 • 1,8 = 175,4
Het 95%-betrouwbaarheidsinterval voor
het gemiddelde is dus ongeveer [175.4, 182.6].
Hij kan concluderen:
"Ik kan met 95% betrouwbaarheid stellen dat het gemiddelde tussen de
175,4 en 182,6 ligt" |
|
| |
| |
|
|
|
| |
|
|
|
OPGAVEN. |
| |
|
|
|
| 1. |
De reactietijd van
180 gamers is getest en daaruit bleek een gemiddelde van 0,78 sec met
een standaardafwijking van 0,15 sec.
Geef het 95%-betrouwbaarheidsinterval dat uit dit onderzoek volgt. |
| |
|
|
|
| 2. |
Na het centraal
examen wiskunde levert een steekproef van het CITO onder 88 deelnemers
op, dat hun gemiddelde een 6,4 is met een standaardafwijking van
0,7.
Geef in drie decimalen nauwkeurig een 95%-betrouwbaarheidsinterval voor
het werkelijk gemiddelde in heel Nederland. |
| |
|
|
|
| 3. |
Een boswachter meet
het gewicht van een groot aantal spreeuwen. Hij vindt een gemiddelde
gewicht van 80 gram met een standaardafwijking van 16 gram.
Het 95%-betrouwbaarheidsinterval voor de hele spreeuwenpopulatie hangt
natuurlijk af van het aantal spreeuwen dat hij gewogen heeft.
Als hij meer spreeuwen heeft gewogen zal het interval smaller worden. |
| |
|
| |
a. |
Hoeveel keer zo smal
is het 95%-betrouwbaarheidsinterval als hij 216 spreeuwen weegt in
plaats van 85 spreeuwen? |
| |
|
|
|
| |
b. |
Hoeveel spreeuwen
heeft hij gewogen als het 95%-betrouwbaarheidsinterval een breedte van 3
gram heeft? |
| |
|
|
|
| 4. |
Examenopgave Havo,
Wiskunde A, 2021-III.
In 2018 hebben 674 leerlingen van een scholengemeenschap een vragenlijst ingevuld.
Zij vormden een aselecte en representatieve steekproef uit de gehele
leerlingenpopulatie van de school. De school kreeg van deze
leerlingen een gemiddelde score van 7,24 op het onderwerp ‘begeleiding’.
Het 95%-betrouwbaarheidsinterval voor de gemiddelde score van alle
leerlingen van de school op het onderwerp
‘begeleiding’ was [7.13 ; 7.35].
Bereken de
standaardafwijking die bij deze steekproef hoort op dit onderwerp.
Geef je antwoord in drie decimalen. |
| |
|
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|