| |
|
| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
 |
|
Formules opstellen en
Ongelijkheden oplossen. |
| |
|
|
|
Hoe je ongelijkheden
moet aanpakken kan ik het beste met een voorbeeld laten zien.
Voorbeeld
Als je veel energie verbruikt is
het misschien voordelig om zonnecollectoren op je dak te laten plaatsen.
De aanschaf en het installeren van zulke panelen kost 30.000,-
maar je kunt erop rekenen dat ze 25 jaar meegaan..
Als je eenmaal zonnepanelen hebt, dan kost het je nog maar 0,17 per kWh
energie, terwijl zonder panelen de prijs ongeveer gelijk is aan
0,42 per kWh.
Stel dat een gezin per jaar x kWh energie verbruikt.
Zonder zonnepanelen zijn de jaarlijkse kosten dan K = 0,42
x
De zonnepanelen zelf kosten per jaar 30000/25 =
1200 en daar komt dan nog 0,17 per kWh bij
Met zonnepanelen zijn de totale kosten dan K = 1200 + 0,17
x |
| |
|
|
|
Als je wilt weten bij
welk verbruik de kosten met zonnepanelen lager zijn dan de kosten zonder
zonnepanelen dan moet dus gelden:
1200 + 0,17x < 0,42x
Dit noemen we in de wiskunde een ongelijkheid. Dat is elke
vergelijking met een < of > of ≤ of ≥ teken.
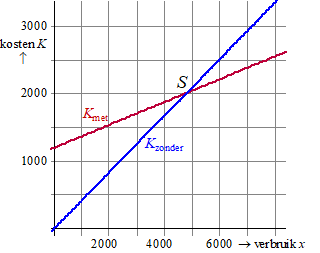
Hiernaast heb ik de grafieken van y = 1200 + 0,17x
en y = 0,42x geplot. Je ziet dat bij laag verbruik
de blauwe grafiek onder de rode ligt. Dan zijn de kosten zonder
zonnepanelen dus lager dan de kosten met zonnepanelen.
Maar vanaf het snijpunt S ligt de rode lijn lager dan de
blauwe dus zijn dan de kosten met zonnepanelen lager. |
 |
| |
|
|
|
Het enige dat we
moeten doen is dus dat snijpunt uitrekenen, en dat gaat met de GR
gelukkig erg makkelijk;
Y1 = 1200 + 0,17X
Y2 = 0,42X
Cacl - intersect levert dan x = 4800 en y = 2016
Dat betekent dat de kosten gelijk zijn bij een verbruik van 4800 Kwh en
die kosten zijn dan 2016 per jaar.
De oplossing van de ongelijkheid is dus x > 4800
(want dan ligt de rode lijn onder de blauwe). |
| |
|
|
|
| |
|
|
|
| |
|
|
|
OPGAVEN. |
| |
|
|
|
| 1. |
Een werknemer wil in
verband met zijn nieuwe baan gaan verhuizen van Groningen naar
Maastricht. Daarvoor zoekt hij een verhuisbedrijf. Hij heeft berekend
dat alles wel in één verhuiswagen kan, en leest de offertes van twee
verhuisbedrijven. Het betreft de bedrijven Budget Verhuisservice en
Mast BV.
Elk bedrijf vraagt voor het gebruik van een verhuiswagen een
vast bedrag per dag. Verder komt daar nog bovenop een bedrag per
kilometer.
Budget Verhuisservice vraagt voor de wagen 400,- en
verder per km nog 2,50.
Mast BV vraagt voor de wagen 550,- en verder per km nog
1,60.
Stel formules op voor de totale vervoerkosten K en de afstand a
en bereken bij welke afstanden welk bedrijf het goedkoopst is. |
| |
|
|
|
| 2. |
Een
automobilist wil een nieuwe auto gaan kopen, maar hij twijfelt
nog tussen een auto die rijdt op benzine en een auto die rijdt
op LPG (gas). LPG is goedkoper: het kost per liter 0,98
terwijl benzine per liter 1,75 kost.
De auto die hij op het oog heeft rijdt op benzine 1 op 14, en
met LPG 1 op 11 (dat betekent dat met 1 liter benzine 14 km
gereden kan worden en met 1 liter LPG 11 km).
Maar de wegenbelasting per jaar is voor benzine 430,- en voor
LPG 910,-.
Neem aan dat de aanschafkosten van de auto's gelijk zijn.
Stel dat de automobilist per jaar k kilometer
rijdt.
Stel formules op voor de totale kosten K per jaar en het
aantal kilometers k, en bereken bij welke aantallen kilometers
per jaar de automobilist het best de LPG auto kan nemen. |
| |
|
|
|
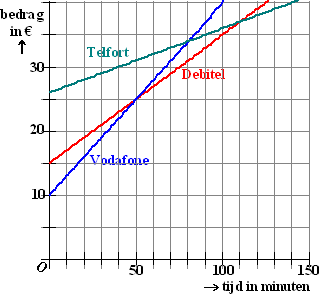
| 3. |
In de
grafieken hiernaast staan de kosten voor een mobiele
telefoon bij drie aanbieders.
Elke aanbieder vraagt een basisbedrag en daarnaast nog een bedrag per
belminuut. |
 |
| |
|
|
| |
a. |
Welke
aanbieder rekent de laagste kosten per belminuut? |
| |
|
|
| |
b. |
Stel voor
elke aanbieder een vergelijking op voor de kosten en het aantal belminuten en bereken vervolgens welke aanbieder
bij welk aantal bel minuten het goedkoopst is. |
| |
|
|
| |
Een nieuwe aanbieder richt
zich op mensen die veel bellen. Deze aanbieder vraagt een
basisbedrag van 30, - |
| |
|
|
| |
c. |
Hoeveel moet men per
belminuut vragen om vanaf 100 belminuten de goedkoopste te zijn? |
| |
|
|
|
| 4. |
De
secretaris van een voetbalvereniging houdt al jaren nauwkeurig bij
hoeveel leden de vereniging heeft. Er zijn twee soorten leden:
jeugdleden en seniorleden.
Beide aantallen zijn in de loop der jaren gegroeid.
Voor de jeugdleden
geldt J = 120 + 14t en voor de seniorleden geldt S = 240 + 8t
Daarin is t de tijd in jaren met t = 0 in 1980. |
| |
|
|
|
| |
a. |
Hoe kun je
zonder een berekening te maken direct aan deze formules zien welk van
beide ledensoorten het snelst groeit? |
| |
|
|
|
| |
b. |
Bereken in
welk jaar er evenveel jeugdleden als seniorleden zullen zijn als deze
groei zo doorgaat. |
| |
|
|
|
| |
c. |
Stel een
formule op voor het totaal aantal leden als deze groei zo doorgaat en
bereken daarmee in welk jaar het totaal aantal leden voor het eerst meer
dan 1800 zal zijn. |
| |
|
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|