| |
© h.hofstede (h.hofstede@hogeland.nl)
|
| Maxima
en Minima. |
|
 |
|
|
|
| Om een top of een dal (maximum of
minimum) van een grafiek te vinden ga je als volgt te werk. |
 |
|
| |
|
| stap 1: |
PLOT de grafiek en zorg dat je het
maximum of minimum in beeld hebt. |
| stap 2: |
Druk op CALC
en kies 3: minimum of 4: maximum |
| stap 3. |
Kies door met de cursorpijltjes omhoog
of omlaag te gaan de juiste formule (zie je boven in beeld)
(opm: als er maar één formule in je GR staat hoef je dit
uiteraard niet te doen) |
| stap 4. |
Je rekenmachine vraagt
nu "Left Bound?"
Ga met de cursor aan de linkerkant van het maximum/minimum staan,
en druk op ENTER |
| stap 5. |
Je rekenmachine vraagt
nu "Right Bound?"
Ga met de cursor aan de rechterkant van het maximum/minimum staan,
en druk op ENTER. |
| stap 6. |
Je rekenmachine vraagt
nu "Guess?"
Ga met de cursor (ongeveer) op het maximum/minimum staan en druk
weer op ENTER.
Dan verschijnen de coördinaten onder in beeld. |
|
|
|
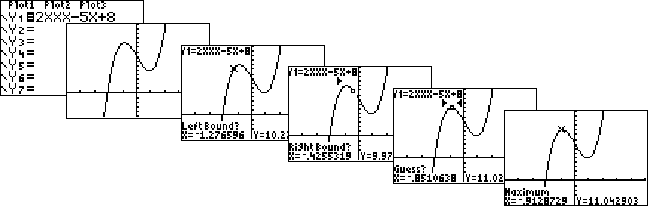
| Voorbeeld:
Zoek de coördinaten van het maximum van de grafiek van y = 2x3
- 5x + 8. |
|
|
|
|
|
|
| Het gezochte maximum is ongeveer
het punt (-0.91, 11.04) |
| |
|
| |
|
|
|
OPGAVEN |
|
|
| 1. |
Bereken de maxima en/of minima van de
grafieken van de volgende formules: |
| |
|
|
|
a. |
y = 4x2 - 5x
+ 8 |
| |
|
|
|
b. |
N = 2t
- 3t |
| |
|
|
| |
c. |
Q = 0,05P3
- 1,3P2 + 0,6P |
| |
|
|
|
d. |
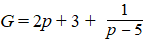 |
|
| |
|
| 2. |
Examenvraagstuk HAVO wiskunde A, 2007. Een hardloopster is gespecialiseerd op
de 100 meter. Bij dit atletiekonderdeel moet je zo
snel mogelijk je topsnelheid halen en die dan proberen vast te houden
tot de finish. Haar trainer heeft haar sprint laten
onderzoeken met behulp van supersnelle camera’s.
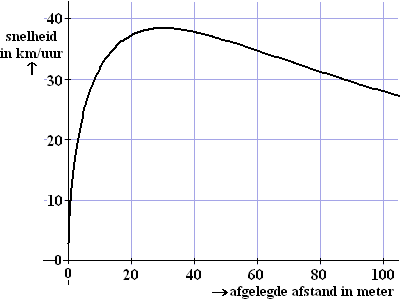
In onderstaande figuur is het verband tussen de snelheid en
de afgelegde afstand in een grafiek
weergegeven. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
Op verzoek van de trainer heeft een
wiskundige een formule gemaakt die goed past bij deze
grafiek.
Die formule is: |
| |
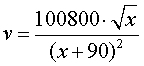 |
| |
|
|
|
| |
In deze formule is v de
snelheid in kilometer per uur en x de
afgelegde afstand in meter.
In de eerste figuur zie je dat de
maximale snelheid ongeveer 38 km per uur is en de snelheid
bij de finish ongeveer 28 km per uur. |
| |
|
|
|
| |
a. |
Bereken met welke snelheid de
hardloopster volgens de formule de finish passeert.
Geef je antwoord in één decimaal. |
| |
|
|
|
| |
b. |
Bereken de hoogste snelheid die de
hardloopster bereikt volgens de formule. Geef
je antwoord in één decimaal. |
| |
|
|
|
| |
In de grafiek zie je dat de snelheid
tijdens een gedeelte van de sprint hoger dan 35
km per uur is. |
| |
|
|
|
| |
c. |
Bereken met behulp van de formule
hoeveel meter de hardloopster aflegt met een
snelheid die hoger is dan 35 km per uur. |
| |
|
|
|
| 3. |
Billie en Bessie Turf
zijn twee gezellige dikkerds. Ze wegen op 1 december (t = 0)
beiden ongeveer 90 kg en hun gewicht is door hun ongezonde leefpatroon
nog steeds continu aan het toenemen.
Daarom besluiten beiden na een poosje toch maar een dieet te gaan
volgen.
Omdat dat moet van hun diëtiste houden ze lange tijd hun gewicht bij, en
de diëtiste stelt na afloop de volgende wiskundige modellen op voor deze
gewichten:
Billie: G
= 90 - 8 • 1,3(-t² +
76t - 1444) + 0,2t
Bessie: G = (0,9t - 14,5) • 2,7(-0,002t² +
0,065t - 0,53) + 98
Daar bij is t = 0 op 1 december, en t is de tijd in dagen.
G is het gewicht in kg. |
| |
|
|
|
| |
a. |
Plot de grafiek van
het gewicht van Billie voor t = 0 tot t = 60, en leg uit wanneer Billie
waarschijnlijk is begonnen aan zijn dieet. |
| |
|
|
|
| |
b. |
Plot in dezelfde
figuur het gewicht van Bessie, en bereken het maximale gewicht van
Bessie. |
| |
|
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|