| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Gemiddelde toenames |
 |
| |
|
|
|
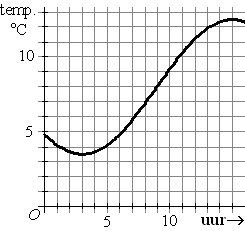
| Hiernaast staat de grafiek van
het temperatuurverloop op 6 februari 1995 in Groningen. Je ziet dat
vanaf middernacht de temperatuur eerst nog wat afneemt, maar vanaf
ongeveer 3 uur gaat toenemen tot maximaal ongeveer 12,5 ºC om 15 uur.
We zijn nu geïnteresseerd in de volgende vraag:
Wat is de gemiddelde toename per uur tussen 3
uur en 9 uur?
We lezen uit de grafiek af dat om 3 uur te temperatuur ongeveer
3,5ºC was en om 9 uur 8 ºC. |
|
De toename is dus 8
- 3,5 =
4,5ºC geweest maar dat was over een periode van 9 - 3 = 6 uur.
De gemiddelde toename was dus 4,5/6 =
0,75 ºC/uur.
Zo. Dat was te doen. Voor de gemiddelde toename deel je gewoon de totale
toename door het aantal uur. Tijd voor de volgende vraag:
"Wat stelt het voor in de grafiek?"
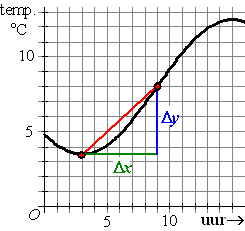
De totale toename was 4,5ºC en die vonden we door 8 - 3,5 te
berekenen. Dat is dus het verschil van beide y-waarden, ofwel
Δy:
het blauwe lijnstukje in de grafiek hiernaast. |
|
Het aantal uur was 6 en dat
vonden we door 9 - 3 te berekenen. Dat is dus het verschil van beide x-waarden,
ofwel
Δx: het groene lijnstukje
in de grafiek. De gemiddelde toename hebben we berekend als
Δy/Δx
en die kennen we nog van vroeger: het is de helling van de lijn tussen
beide punten.
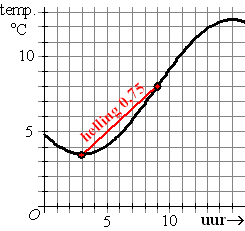
Conclusie: de helling van de rode lijn is 0,75
| De
gemiddelde toename tussen twee punten van een grafiek
is de helling van de rechte lijn daartussen. |
Deze gemiddelde toename heet ook
wel het differentiequotiënt.
Als je een formule voor de grafiek hebt, dan hoef je de y-waarden
natuurlijk niet af te lezen maar kun je ze gewoon berekenen, dat is veel
nauwkeuriger.
Dit is allemaal hetzelfde:
|
|
| |
|
|
|
| • |
gemiddelde toename tussen punt A en punt B |
| • |
differentiequotiënt op interval [xA,
xB] |
| • |
helling van lijnstuk AB |
| • |
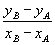 |
|
|
| |
|
|
|
|
Speciaal
geval: Als y de afstand voorstelt en x de tijd. |
| |
|
|
|
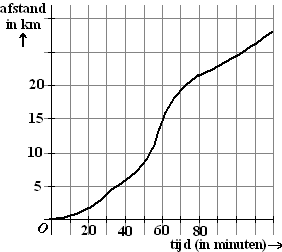
n de grafiek
hiernaast staat op de x-as de tijd dat iemand aan het fietsen is, en op de y-as
de afstand die hij heeft afgelegd.
We berekenen het differentiequotiënt tussen x = 20 en x =
60
Bij x = 20 hoort ongeveer y = 2 en bij x = 60 hoort
ongeveer y = 15
Dat geeft voor het differentiequotiënt (15 - 2)/(60
- 20) = 13/40 = 0,325
Die 0,325 is dus de totale afgelegde afstand (13 km) gedeeld door de
totale tijd (40 minuten). In dit geval 0,325 km per minuut. Maar
dat is de snelheid (immers snelheid is afstand gedeeld door tijd)
Kortom, de gemiddelde snelheid tussen 20 en 60 minuten is 0,325 km/min.
(dat is 19,5 km/uur)
Bij een tijd-afstand grafiek is het
differentiequotiënt
de gemiddelde snelheid. |
|
 |
| |
|
|
|
| |
|
|
|
OPGAVEN. |
| |
|
|
|
| 1. |
a. |
Gegeven is de formule
N = 4t + 2√t
.
Bereken het differentiequotiënt op interval [3, 8] in twee
decimalen nauwkeurig. |
| |
|
|
|
| |
b. |
Gegeven is de formule
P(t)
= 5t - 2/t
Bereken het differentiequotiënt op interval [-5, -2] in
twee decimalen nauwkeurig. |
| |
|
|
|
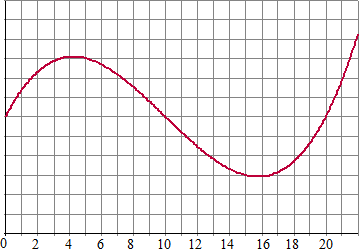
| 2. |
Hiernaast staat de
grafiek van een formule f. |
 |
| |
|
|
| |
a. |
Bereken de gemiddelde toename
tussen x
= 12 en x = 20 |
| |
|
|
| |
b. |
Noem drie intervallen waarop het
differentiequotiënt gelijk is aan nul. |
| |
|
|
|
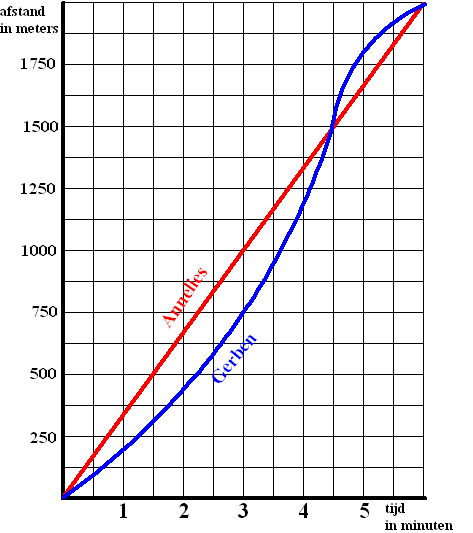
| 3. |
Annelies en haar broer Gerben
gaan met de fiets naar school.
De afgelegde weg s als functie van de tijd t staat in de
grafiek hieronder. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
a. |
Bereken voor Annelies
de gemiddelde snelheid. |
| |
|
|
|
| |
b. |
Wie rijdt de eerste twee minuten
gemiddeld het
snelst? |
| |
|
|
|
| |
c. |
Wie rijdt tussen t =
3,5 en t
= 4 het snelst? Hoe zie je dat aan de grafiek? |
| |
|
|
|
| |
d. |
Wanneer passeert Gerben Annelies? Hoe zie
je aan de grafiek dat hij op dat moment sneller rijdt? |
| |
|
|
|
| |
e. |
Bepaal zo goed
mogelijk met welke snelheid Gerben fietst op het moment dat hij Annelies
inhaalt. |
| |
|
|
|
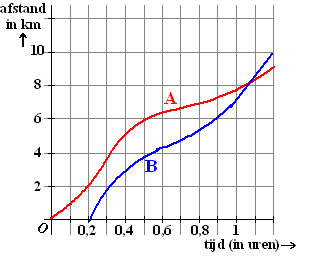
| 4. |
Hiernaast zie je de
grafiek van twee joggers (mevrouw A en mevrouw B) die hetzelfde
parcours lopen. Zoals je ziet vertrekt mevrouw B later dan
mevrouw A. |
|
| |
|
|
| |
a. |
Bereken de gemiddelde snelheid van
mevrouw B gedurende het eerste half uur dat zij loopt. |
| |
|
|
| |
b. |
Bereken de gemiddelde snelheid
van mevrouw A gedurende het tweede half uur dat zij loopt. |
| |
|
|
|
| |
c. |
De beide dames hebben een
loophorloge om met GPS functie. Dat horloge geeft o.a. hun
gemiddelde snelheid vanaf het begin aan.
Op welk moment tijdens haar loop geeft het
horloge van mevrouw A de grootste gemiddelde snelheid
aan? |
| |
|
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|