| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Standaardafwijking |
 |
| |
|
|
|
We hebben al twee
manieren besproken om iets over de breedte van een verdeling te
zeggen, en dat zijn de spreidingsbreedte en de kwartielafstand.
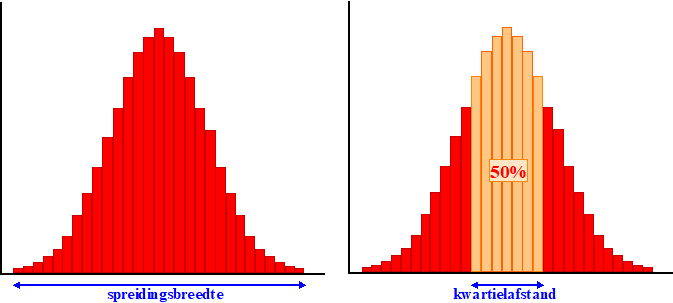
De spreidingsbreedte was gewoon de totale breedte, en de kwartielafstand
was de breedte van de middelste 50% van alle metingen (de afstand
tussen het eerste kwartiel en het derde kwartiel).
Hieronder zie je beiden bij een symmetrische verdeling
weergegeven: |
| |
|
|
|
|
 |
| |
|
|
|
Beiden hebben hun
voor- en nadelen.
De spreidingsbreedte heeft het nadeel dat één klein staafje ver naast de
rest (een "uitschieter") de breedte nogal kan beďnvloeden.
Maar ja, de kwartielafstand heeft weer het nadeel dat maar de helft van
alle metingen wordt meegeteld.
Er is een soort tussenvorm te gebruiken, die toch een iets groter deel
van de metingen meetelt, en dat is de
standaardafwijking. Daar wordt meestal de letters
s (de Griekse s) voor
gebruikt.
Ik kan alvast zeggen dat de standaardafwijking in de meeste steekproeven
ongeveer 70% van de metingen meetelt, maar in de volgende les zullen we
daar verder op in gaan.
Deze les gaan we verder bekijken hoe je die standaardafwijking met je GR
kunt berekenen.
Neem de volgende frequentietabel van de eindrapportcijfers van een klas: |
| |
|
|
|
| cijfer |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| frequentie |
1 |
2 |
6 |
10 |
12 |
5 |
3 |
1 |
|
| |
|
|
|
Voer de cijfers in in
de lijsten van je GR:
STAT - EDIT
L1 = 3, 4, 5, 6, 7, 8, 9, 10
L2 = 1, 2, 6, 10, 12, 5, 3, 1
STAT - CALC - 1: 1-Var-Stats en dan:
List: L1
FreqList: L2
Calculate
ENTER geeft dan een hele lijst gegevens.
Eentje daarvan is σx = 1.465435089
Dat is de standaardafwijking. |
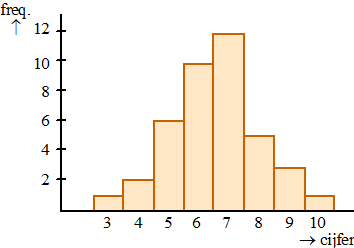 |
Wat houdt
dat dan ongeveer in?
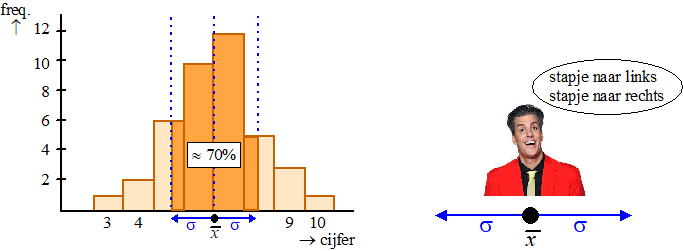
Als je vanaf het gemiddelde (dat is 6,55 dat is de bovenste van de lijst
getallen in je GR) een stapje van grootte s
naar rechts gaat en ook een stapje van grootte s
naar links, dan zit daartussenin ongeveer 70% van al je metingen.
Dat staat getekend in onderstaande figuur. |
| |
|
|
|
|
 |
| |
|
|
|
| Bedenk:
|
|
•
•
• |
Die 70% is
ongeveer.
We gebruiken dit vooral bij ongeveer symmetrische verdelingen. Meer
daarover in de volgende les.
s is een maat voor de breedte
van de verdeling. Hoe groter s, des te breder
is het histogram |
| |
|
|
|
Klassenindelingen.
Nou daar valt niet veel nieuws over te melden.
Het enige is dat je bij het invoeren in de GR moet doen alsof alle
metingen het klassenmidden zijn.
Dus bij L1 zet je de klassenmiddens.
|
klassenindeling:
klassenmiddens gebruiken ! |
|
| |
|
|
|
| |
|
|
|
OPGAVEN. |
| |
|
|
|
| 1. |
Een atlete heeft tijdens 10 achtereenvolgende
trainingen steeds direct na een 400-meterloop haar polsslag
gemeten.
Dat leverde de volgende serie waarden op:
100 - 112 - 120 - 105 -
145 - 132 - 110 - 156 - 194 - 134 |
| |
|
|
|
| |
a. |
Bereken de
standaardafwijking van
deze waarden. |
| |
|
|
|
| |
b. |
De waarde 194 is wel érg
hoog. De atlete vermoedt daarom dat zij een meetfout heeft gemaakt. Hoe
groot zou de standaardafwijking zijn geweest zonder deze
meetwaarde? |
| |
|
|
|
| 2. |
In de volgende tabel staan de
hoogten van een groot aantal bomen in een bos. |
| |
|
|
|
| |
| hoogte |
4-<8 |
8-<12 |
12-<16 |
16-<20 |
20-<24 |
24-<28 |
28-<32 |
32-<36 |
36-<40 |
| frequentie |
14 |
20 |
36 |
58 |
43 |
22 |
12 |
8 |
2 |
|
| |
|
|
|
| |
a. |
Bereken de
standaardafwijking van
deze hoogten. |
| |
|
|
|
| |
b. |
Controleer of de
70%-regel ongeveer klopt. |
| |
|
|
|
| |
c. |
Hoe groot zou de standaardafwijking
zijn als een klassenbreedte van 8 was gekozen in plaats van 4?
Bereken dat voor het geval de eerste klasse gelijk is aan
0-<8 |
| |
|
|
|
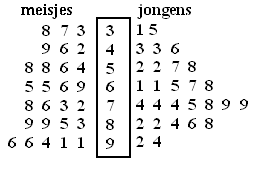
| 3. |
In het dubbele steel-
en bladdiagram hiernaast staan de proefwerkcijfers van een klas,
gesplitst naar meisjes en jongens. |
 |
| |
|
|
| |
a. |
Probeer zonder een berekening te
maken in te schatten wie de grotere standaardafwijking
heeft (de jongens of de
meisjes). |
| |
|
|
|
| |
b. |
Controleer je antwoord
op de vorige vraag met een berekening. |
| |
|
|
|
| |
c. |
Ga met een berekening
na of de standaardafwijking van de hele groep jongens en meisjes sámen
gelijk is aan de standaardafwijking van de jongens plus die
van de meisjes. |
| |
|
|
|
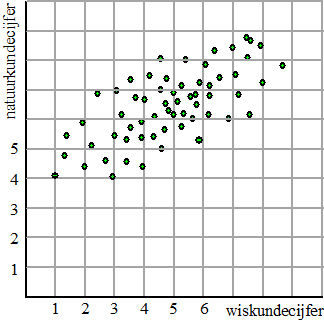
| 4. |
Hieronder staan van een grote groep studenten de cijfers voor een wiskundetoets en een natuurkundetoets. |
| |
|
|
|
| |
 |
| |
|
|
|
| |
a. |
Welk toets had het hoogste gemiddelde? Leg uit! |
| |
|
|
|
| |
b. |
Welke toets had de grootste standaardafwijking? Leg uit! |
| |
|
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|