© h.hofstede (h.hofstede@hogeland.nl)

 
Groeifactoren bij andere tijdseenheden.
Laten we gaan proberen een formule te maken bij onderstaande tabel.
x 5 8 11 14
y 47,19 193,27 791,65 3242,59
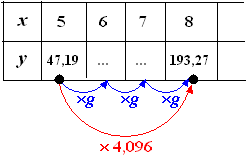
et lijkt erop dat deze tabel een exponentiële functie beschrijft, want de factoren zijn achtereenvolgens: 
193,27/47,19 = 4,096 en  791,65/193,27 = 4,096 en  3242,59/791,65 = 4,096  en die zijn allemaal gelijk.
Toch is 4,096 niet de groeifactor g die bij deze tabel hoort!

Waarom dan niet?

Dat komt omdat de x-waarden niet stapjes van één nemen, maar stapjes van drie. En de groeifactor g is het getal waarmee je y vermenigvuldigt als x één toeneemt. Hoe vinden we de g voor een stapje van één?
Nou simpel, denk de rest van de tabel erbij:
x 5 6 7 8 9 10 11 12 13 14
y 47,19 .... .... 193,27 .... .... 791,65 .... .... 3242,59
Omdat deze tabel stapjes van één neemt, zijn de getallen waarmee de y-waarden worden vermenigvuldigd wél gelijk aan de groeifactor g. Kijk bijvoorbeeld tussen x  = 5 en x = 8 hiernaast.
Daarin zie je dat  ×g   ×g   ×g   precies hetzelfde moet zijn als  ×4,096
Dat betekent dat  g3  = 4,096
Ofwel:

omdat stapjes van 3 zijn genomen vinden we g3
Hoe maken we daar g van?
Da's makkelijk.
Daar hebben we de GR voor.

Voer in:   Y1 = X^3  en  Y2 = 4,096
Dan vind je via intersect  dat bij het snijpunt geldt X = 1,6 en dat is de gezochte g.


Twee soorten vragen.

vraag 1:  van kortere naar langere tijd
Stel dat de groeifactor per week gelijk is aan 1,004.
Hoe groot is dan de groeifactor per jaar?

Nou voor een jaar moet je die vermenigvuldiging met 1,004 dus 52 keer doen.
Dat geeft in totaal  gjaar = gweek52  = 1,00452 = 1,23

vraag 2:  van langere naar kortere tijd.
Stel dat de groeifactor per week gelijk is aan  1,26.
Hoe groot is dan de groeifactor per dag?

Als je die groeifactor per dag 7 keer doet dan heb je de groeifactor per week
Dat geeft dan   gdag7 = gweek ofwel   gdag7 = 1,26
Y1 = 1,26 en Y2 = X^7  en dan intersect geeft  X = gdag = 1,034
 
Voorbeeldje dat vaak verkeerd gaat.

Een bank geeft  24% rente per jaar.  Hoeveel procent per maand is dat?

foute oplossing:  24/12 = 2% per maand.

goede oplossing:  24%  betekent dat g = 1,24
voor een maand geldt  gmaand12  = gjaar
gmaand12 = 1,24
Y1 = X^12  en  Y2 = 1,24  en dan intersect geeft 1,018
De rente per maand is dus  1,8%
 
   
 
 
  OPGAVEN.
1. Laat zien dat er sprake is van exponentiële groei en geef de groeifactor bij de volgende tabellen:
x 10 15 20 25 30
y 12,84 4,22 1,38 0,45 0,147
x 4 11 18 25 32
y 2,43 3,42 4,81 6,77 9,53
x 6,0 8,5 11,0 13,5 16,0
y 6,77 5,34 4,21 3,31 2,61
x 2,5 3,9 5,3 6,7 8,1
y 19,21 16,58 14,30 12,34 10,65
 
2. Geef de groeifactor in de volgende gevallen.
   
a. De groeifactor per dag is  4,3. Hoe groot is de groeifactor per uur?
   
b. De groeifactor per minuut is 1,03. Hoe groot is de groeifactor per uur?
   
c. De groeifactor per week is 8. Met hoeveel procent neemt het per dag toe?
   
d. Iets neemt af met 5,4% per uur. Wat is de groeifactor per dag?
   
e. Iets neemt toe met 12% per week, hoe groot is de groeifactor per dag?
   
f. Iets verdubbelt elke week. Hoeveel procent toename is dat per uur?
   
3. Een artikel is nu al vier maanden achter elkaar met hetzelfde percentage in prijs verlaagd. Na drie maanden was er al 51% van de oorspronkelijke prijs afgegaan.
Hoeveel is er na 4 maanden van de oorspronkelijke prijs afgegaan?
   
4.

Examenvraagstuk HAVO Wiskunde B, 2007

Wanneer de hoogte toeneemt, neemt de luchtdruk af. Deze afname van de luchtdruk verloopt exponentieel. De luchtdruk kan worden gemeten in mm Hg (Hg staat voor kwik).

Op een gegeven moment is op een bepaalde plaats de luchtdruk op zeeniveau (hoogte = 0) gelijk aan 760 mm Hg en op één kilometer hoogte is deze gelijk aan 648 mm Hg. Volgens het exponentiële model is de luchtdruk op 100 meter hoogte vrijwel gelijk aan 748 mm Hg.
   
  Toon dit door middel van een berekening aan.
       
5. Examenvraagstuk HAVO Wiskunde A, 2010.

China ontwikkelt zich in hoog tempo tot grootmacht, ook op het militaire vlak. Het Pentagon, het Amerikaanse Ministerie van Defensie, houdt de Chinese defensie-uitgaven nauwlettend in de gaten. In onderstaande figuur staan de Chinese defensie-uitgaven volgens China zelf en volgens twee schattingen van het Pentagon, een hoge en een lage. Duidelijk is te zien dat het Pentagon uitgaat van veel hogere defensie-uitgaven dan China opgeeft.
       
 

       
  Volgens het Pentagon namen de defensie-uitgaven in de periode van 2001 tot 2005 exponentieel toe. De hoge schatting steeg van 65 miljard dollar in 2001 tot 93 miljard dollar in 2005.
       
  a. Bereken het jaarlijkse groeipercentage dat het Pentagon als uitgangspunt nam voor de hoge schatting (in deze periode). Geef je antwoord in één decimaal nauwkeurig.
       
  In 2005 was de lage schatting 65 miljard dollar en de hoge 93 miljard dollar, een verschil van 28 miljard dollar. Voor de jaren na 2005 voorspelde het Pentagon dat de defensie-uitgaven exponentieel zouden blijven toenemen. Voor de lage schatting (in deze periode) ging het Pentagon uit van een jaarlijkse groei van 8,5% en voor de hoge schatting van 9,5%.
       
  b. Bereken in welk jaar het verschil tussen de lage en de hoge schatting voor het eerst meer dan 50 miljard dollar zal zijn.
       
 

© h.hofstede (h.hofstede@hogeland.nl)