| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Bewijzen uit het ongerijmde. |
| |
|
|
|
In deze les uit de logica serie ontdekten we dat je een "ALS A DAN
B" bewering mag omdraaien en voor beide beweringen NIET zetten.
Dan blijft het resultaat logisch gelijk.
Deze
"omkering-met-NIET-ervoor" geeft ineens de mogelijkheid een
bewering te bewijzen!
Stel dat ik bewering A wil bewijzen. Dan laat ik zien dat
uit ¬A een foute bewering volgt.
¬A ⇒ B is immers gelijkwaardig met ¬B
⇒ ¬¬A = A. Dus als ik zeker weet dat B
fout is, dan is ¬B waar, en dus A ook.
Zo'n bewijs heet een "bewijs uit het ongerijmde" of
wat mooier gezegd "reductio ad absurdum"
Een bewijs uit het ongerijmde klinkt altijd als volgt:
|
"Stel dat bewering A NIET waar zou zijn
en daar volgt B uit.
Als dan B is duidelijk flauwekul is, moet A wel waar zijn". |
Het werkt vooral als de bewering
¬A makkelijker is aan te pakken dan de bewering A.
Beroemd Voorbeeld: Stevin's Hellend Vlak
De "Beghinselen der
Weeghconst" van Simon Stevin werd in 1586 uitgegeven (in één
band met "De Weeghdaet", "De Beghinselen des Waterwichts",
en een "Anhang" en in 1605 kwam er nog een "Byvough"). Het
behandelt de theorie van krachten die elkaar in evenwicht houden. Zoiets als wat
wij nu statica zouden noemen.
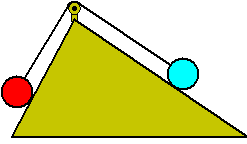
Een klassiek en antiek probleem was : "Evenwicht op een hellend vlak"
|
Twee bollen, verbonden door een touw via een
katrol hangen rusten op twee vlakken met verschillende hellingshoeken.
(het touw en de katrol zijn gewichtloos en alles beweegt wrijvingsloos
uiteraard)
Wanneer is er evenwicht?
Stevin zegt in zijn "Voorstel 19":
|
| Ghelijck des driehoucx rechter sijde
tot de slincker, also t'staltwicht
des cloots op de slincker sijde, tottet staltwicht des cloots
op de rechter sijde. |
|
|
|
 |
Zo. Daar kun je 't
mee doen.
Hij bedoelt natuurlijk te zeggen dat er evenwicht is als de verhouding van de
gewichten gelijk is aan de verhouding van de lengte van de zijden waarop
zij rusten.
Als bijv. de rechterzijde dubbel zo lang is als de linkerzijde, dan moet
voor evenwicht het blauwe gewicht ook dubbel zo groot zijn als het
rode. |
| Stevin geeft als bewijs het beroemde 'clootcrans-bewijs'
met de "bollenkrans" hiernaast. Hij was er zó mee in zijn
nopjes dat de figuur hiernaast zelfs zijn logo is geworden..
STEL dat er géén evenwicht is (het ongerijmde)....
Dan zou de ketting gaan bewegen (geen wrijving!)
Maar in die nieuwe situatie zou er nog steeds geen evenwicht zijn, dus de
ketting zou alsmaar door blijven bewegen.
We hebben een Perpetuüm Mobile!!
|
| "...ende de clooten sullen
uyt haer selven een eeuwich roersel
maken, t'welck valsch is". |
|
|
|
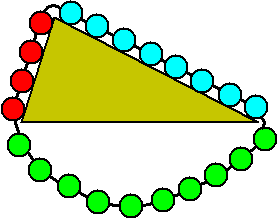 |
Er moet wel evenwicht zijn.
(Het aantal bollen is uiteraard evenredig met de lengte van de zijde). |
|
| |
|
|
|
Dit is een voorbeeld
van een "gedachtenexperiment", waar ik later nog een hele les aan zal
besteden.
Nog een beroemd voorbeeld.
Stelling: |
|
√2 is niet als breuk te schrijven |
|
Bewijs.
Stel dat het wel kan...... (je wist al dat dit bewijs zo zou beginnen)
Dan zijn er gehele getallen p en q te vinden zo, dat
√2
= p/q
Vermenigvuldigen met q geeft q√2
= p, en dat kwadrateren geeft 2q2 = p2
Laten we p en q gaan ontbinden in factoren.
Hoeveel 2en staan er dan in bovenstaande vergelijking?
p2 heeft een even aantal factoren 2 (namelijk het dubbele van
het aantal in p)
q2 ook.
Maar door die ene 2 links extra staan er dan aan de linkerkant een
oneven aantal 2en en aan de rechterkant een even
aantal.
Dat kan niet! De gewenste flauwekul is bereikt!!!
q.e.d. |
| |
|
|
|
|
Contra-Positief. |
| |
|
|
|
| Er is een tweede soort "bewijs uit het ongerijmde"
die erg veel lijkt op de hierboven genoemde, maar er is een subtiel verschil. We
wilden hierboven bewering A bewijzen, en begonnen dan met ¬A
en hoopten dat daaruit "iets" tegenstrijdigs zou volgen. Het was
alleen niet direct duidelijk wat dat "iets" dan zou moeten zijn. |
| |
|
|
|
Het kan ook
directer.
Zo'n bewijs heet "Contra-positief"
, en gaat als volgt:
We zagen al dat uit A ⇒
B volgt ¬B ⇒
¬A.
Dus als we kunnen bewijzen dat uit ¬B volgt dat ¬A, dan hebben
we de bewering A ⇒
B ook bewezen. Let wel: we bewijzen dus niet een bewering A, maar
een bewering van de vorm "Als A dan B". We zeggen niets
over het al of niet waar zijn van A, alleen over de gevolgtrekking
(als A waar zou zijn, dan is B ook waar). Het doel is hier steeds
duidelijk: probeer ¬A aan te tonen.
"Ho stop eens," hoor ik je al zeggen. "Hierboven bij de
ongerijmde bewijzen stond óók een als... dan... bewering (namelijk de
vierde)". Toch was de aanpak daar anders. Kijk maar:
A = "in een driehoek geldt a2 + b2
= c2"
B = "de driehoek heeft een rechte hoek".
Contra-positief gaat het zó:
Neem een driehoek zonder rechte hoek, en probeer te bewijzen dat dan a2
+ b2 ≠
c2
In symbolen: ¬B ⇒
¬A.
Uit het ongerijmde gaat het zó:
Neem een driehoek zonder rechte hoek waarin geldt a2 + b2
= c2 en probeer op flauwekul uit te komen.
In symbolen: (¬B én A) ⇒
onzin (maar wélke onzin is nog onbekend)
Voorbeeldje.
Toon aan: Als (n mod 4) = (2 of
3) dan is n géén kwadraat.
Bewijs:
De contra-positieve variant luidt: "Als n een kwadraat is,
dan is n(mod 4) gelijk aan 0 of 1".
Stel n = k2
, dan zijn er vier gevallen:
|
| 1. |
k (mod 4) = 0
Dan is k = 4q en k2 = (4q)2
= 16q2 = 4 • (4q2 ) dus
is n (mod 4) = 0 |
| 2. |
k (mod 4) = 1
Dan is k = 4q + 1 en k2 = (4q +
1)2 = 16q2 + 8q + 1 = 4 • (4q2
+ 2q) + 1 dus n (mod 4) = 1 |
| 3. |
k(mod 4) = 2
Dan is k = 4q + 2 en k2 = (4q
+ 2)2 = 16q2 + 16q + 4 = 4 • (4q2
+ 4q + 1) dus n (mod 4) = 0 |
| 4. |
k (mod 4) = 3
Dan is k = 4q + 3 en k2 = (4q
+ 3)2 = 16q2 + 24q + 9 = 4 • (4q2 +
6q + 2) + 1 dus n (mod 4) = 1 |
| q.e.d. |
| |
|
|
|
| |
|
|
|
|
OPGAV EN |
| |
|
|
|
| 1. |
We gaan in
deze opgave aantonen dat de vergelijking x3
+ x + 1 = 0 geen breuk als oplossing heeft.
Dat gaat in drie stappen. |
| |
|
|
|
| |
a. |
Stel dat er
wel een oplossing x = p/q
is, en vereenvoudig die zoveel mogelijk.
Vul die oplossing in de vergelijking in, en schrijf je resultaat
zo eenvoudig mogelijk en zonder haakjes en breuken. |
| |
|
|
|
| |
b. |
Onderzoek
van elke van de drie termen van je resultaat of die term even of
oneven is (afhankelijk van het even/oneven zijn van p en
q) |
| |
|
|
|
| |
c. |
Maak het bewijs af. |
|
| |
|
|
|
| 2. |
Dubbelschaak.
Het spel
dubbelschaken heeft dezelfde regels als gewoon schaken,
met als enige verschil dat elke speler als hij aan de beurt is
twee zetten moet doen in plaats van één.
Bewijs dat er voor wit een strategie moet bestaan waarmee hij
nooit verliest. |
| |
|
|
|
| |
|
|
 |
|
| |
|
|
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|