|
|||||
| Een wandelende toren. | |||||
|
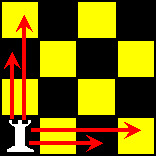
Op een mini-schaakbord van 4 bij 4 staat linksonder in de hoek een toren. Een toren mag bij schaken alleen horizontaal en verticaal bewegen, zoveel velden als je maar wilt. Alleen onze toren mag niet naar een aangrenzend veld, dus al zijn zetten moeten 2 of meer velden beslaan. Kan deze speciale toren een serie van 16 zetten doen zodat
hij elk veld van het bord een keer aandoet en weer eindigt op het veld
linksonder? |
|
||||
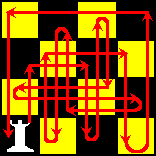
| Tja; dat kun je natuurlijk gewoon
gaan proberen.... Je zou zelfs de oplossing zoals hiernaast nog
best kunnen vinden. Maar ja, dat is voor grafendeskundigen zoals wij intussen zijn natuurlijk ver onder ons niveau!! Zomaar proberen...Bah!! En niet eens een symmetrische route!! Wij als ervaren grafenologen zien natuurlijk direct dat de vraag eigenlijk niets anders is dan "Is er een Hamiltonroute?" |
|
||||
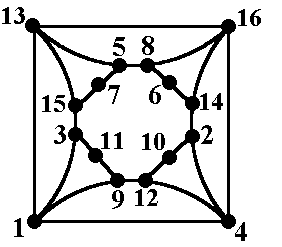
| Laten we daarom van het 4 bij 4 schaakbord een graaf maken met als
knooppunten de velden en als verbindingslijn de relatie
"Staat via een torenzet in verbinding met". Dat geeft de volgende graaf: |
|
||||
|
|
|||||
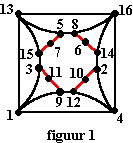
| Laten we proberen een
symmetrische route te ontwerpen...... De punten 11, 10, 6 en 7 graad 2 hebben, dus die verbindingen moeten in ieder geval gebruikt worden. Zie figuur 1. |
|
||||
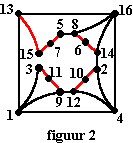
| Verder moeten we de binnenste achthoek verbinden met de buitenkant. Daarvoor kiezen we willekeurig (de zaak is toch symmetrisch) de verbinding 13-15. Maar dan kunnen we 13-5 niet gebruiken want dat maakt een gesloten circuit, en dat kunnen we nooit als deel van een geheel doorlopen zonder een knooppunt dubbel te bezoeken. Verder valt 15-3 ook af; dat zou drie wegen in punt 15 geven. Zie figuur 2. |
|
||||
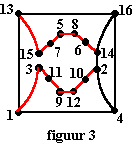
| 1-3 zal in ieder geval gebruikt moeten worden
en dan valt 1-9 af en dan moet 9-12 gebruikt worden en dan valt
12-4 af. 5-8 moet ook gebruikt worden en dan valt 8-16 af. Dat levert de tussenstand hiernaast |
|
||||
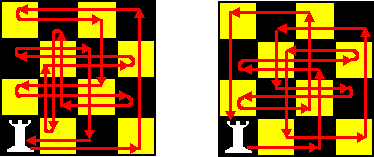
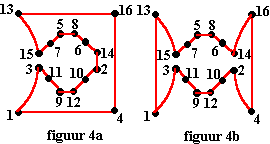
| En nu staan we voor een keuze: 14-2 gebruiken
of niet? Als we 14-2 wel gebruiken vallen 2-4 en 14-16 af en krijgen we de graaf van figuur 4a. Als we 14-2 niet gebruiken moeten we 2-4 en 14-16 wel gebruiken. Dat levert de graaf van figuur 4b. En daarmee zijn de enige twee symmetrische oplossingen gevonden! Ze corresponderen met de twee torenwandelingen hieronder. |
 |
||||
|
|
|||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||