| |
©
h.hofstede (h.hofstede@hogeland.nl) |
| Rekenen
met machten (1) |
 |
|
|
|
Voor we gaan beginnen met
exponentiλle systemen moet je eerst een paar eenvoudige
basisberekeningen met machten kennen en kunnen gebruiken.
Eerst wat namen:
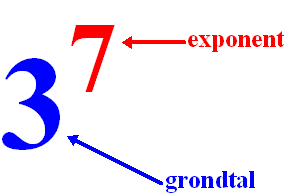
Als je iets tot de macht gaat nemen dan heet dat
machtsverheffen.
Het getal dat op de grond staat heet het
grondtal en het getal dat in de lucht hangt heet de
exponent. |
|
|
| Waarschuwing vooraf: |
|
Machtsverheffen gaat vσσr vermenigvuldigen ! |
|
| |
|
Veelgemaakte blunders:
Omdat machten vσσr vermenigvuldigen gaan kun je niet zeggen:
5 43 = 203 want je mag niet eerst 5 4
uitrekenen voordat je die macht doet.
Een ook met letters geldt dus NIET dat 3 5x
= 15x |
 |
| |
|
Wat wel mag:
Natuurlijk geldt nog wel onze oude algebraregel dat je blokjes met
precies dezelfde letters kunt samennemen.
Dus net zoals 2x + 3x = 5x geldt ook
4 3x + 3 3x = 7 3x |

|
| |
|
|
1. machten
vermenigvuldigen (en een beetje delen). |
|
|
|
Wat gebeurt er als je twee machten met het
zelfde grondtal met elkaar vermenigvuldigt?
Met getallen is het simpel: 35 34
= (3 3 3 3 3) (3 3 3 3) = 3 3 3
3 3 3 3 3 3 = 39
Waar komt het op neer: Als de grondtallen gelijk zijn kun je
machten die met elkaar worden vermenigvuldigd samennemen. Dat doe je
door de exponenten op te tellen. In formule: |
|
|
|
|
| |
|
Voorbeelden:
24 26 = 210
82 6 85 = 6 87
4x2 3x7 = 12x9
3p p4 = 3p5 |
|
|
|
|
Andersom kan het ook: als de machten gelijk zijn
maar de grondtallen verschillend kun je ze ook samennemen,
bijvoorbeeld:
34 24 = 3 3 3
3 2 2 2 2 = (3 2) (3 2) (3 2) (3
2) = 6 6 6 6 = 64
In formulevorm: |
| |
|
| |
|
| |
|
Voorbeelden;
25 65 = 125
43 7 33 = 7 123
x4 10 y4 = 10 (xy)4
|
|
|
| |
|
| |
machten
delen. |
| |
|
| |
Als je zou moeten gokken dan zou je het vast
goed doen! In dit geval wel denk ik.
Als termen met elkaar vermenigvuldigen betekent dat hun hun machten moet
optellen, wat zou termen op elkaar delen dan betekenen?
Zie je wel: Je gokt dat de machten dan wel van elkaar afgetrokken
zullen worden.
En dat is ook zo! |
| |
|
| |
|
| |
Ik hoop dat je dat ook logisch vindt.
Stel dat je bijvoorbeeld g7 moet delen door g4
Dat geeft dan: |
| |
 |
| |
|
| |
Van die zeven g's bovenin vallen er 4
weg tegen die ondersten, dus blijven er drie over. |
|
|
| 2. machten van machten. |
|
|
|
Als je iets tot-de-macht doet, en dan het resultaat wιιr
tot de macht gebeurt er dit:
(32)4 = (iets)4 = (iets) (iets)
(iets) (iets) = 32 32 32
32 = (3 3) (3 3) (3 3) (3 3)
= 38
Je ziet dat je in dit geval de exponenten met elkaar moet
vermenigvuldigen: |
|
|
|
|
| |
|
| |
Denk er om dat de regel beide
kanten op gebruikt kan worden!! |
| |
|
Voorbeelden;
(34)5 = 320
24x = (24)x = 16x
(p2)7 = p14
(5a3)4 = 54 (a3)4
= 625a12
(3x)2 = 32x |
|
| |
|
| Zorg dat je, vσσr je met de
volgende opgaven begint, alle voorbeelden hierboven goed begrijpt!! |
| |
|
Moeilijk voorbeeld.
4 32x + 5
= 4 32x 35
= 4 (32)x 243
= 972 9x |
|
| |
| |
|
|
|
OPGAVEN |
|
|
| 1. |
Schrijf de volgende uitdrukkingen in de vorm y
= a gx en zo eenvoudig mogelijk: |
|
| |
|
| a. |
y = 4 32x
|
| |
|
| b. |
y = 0,5 4x +
2 |
| |
|
| c. |
y = 3 22x
2 |
| |
|
| d. |
y = 5 4x 4x
+ 1 |
| |
|
| e. |
y = 0,22x + 3 |
| |
|
| f. |
y = 20 34x + 5 |
| |
|
| g. |
y = 2x 22x
4 |
| |
|
| h. |
y = 6x 3 6x+1 |
| |
|
| i. |
y = 3 1,82x
6 1,8x + 1 |
|
| |
|
|
|
| 2. |
Herleid de volgende formules: |
| |
|
|
|
| |
a. |
P = (4t)3 - 6t3 |
| |
|
|
| |
b. |
Z = (2x)4 + 2x 4x3 |
| |
|
|
|
| |
c. |
G = 2m3 5m4 + (2m)5
m2 |
|
| |
|
|
|
| |
d. |
y = (2x2)3
- 4x4 x2 |
|
| |
|
|
|
| 3. |
Schrijf zo eenvoudig mogelijk: |
| |
|
|
|
| |
a. |
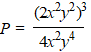 |
| |
|
|
|
| |
b. |
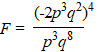 |
| |
|
|
|
| |
c. |
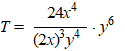 |
| |
|
|
|
 |
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
|
|
|