| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Matchings. |
| |
|
|
|
Voordat we
ingewikkelder roosterproblemen gaan bekijken moeten we ons eerst
verdiepen in Matchings.
We beginnen, zoals intussen gebruikelijk, maar weer met een zooi termen.
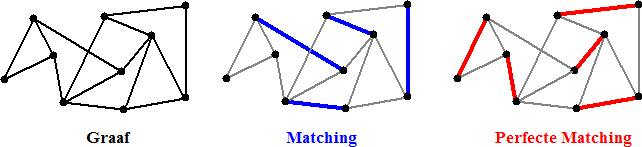
Een matching M van een graaf G is een verzameling verbindingslijnen van
G die "nergens bij elkaar komen". Dat betekent dat er geen enkel
knooppunt van G is dat aan twee van die lijnen vastzit. Een matching
noemen we perfect als elk
knooppunt van G ergens aan een lijn van M vastzit. |
| |
|
|
|
|
 |
| |
|
|
|
| |
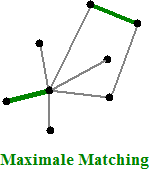
Een perfecte matching
is trouwens wat anders dan een maximale
matching. Hiernaast zie je een graaf met een maximale matching (groter
kan niet) die toch niet perfect is.
Een alternerend pad in een
graaf G met matching M is een pad waarvan de wegen om en om wél en niet
bij de matching M horen. Een
M-vergrotend pad is een alternerend pad waarvan begin- en
eindlijn niet bij M horen.
Zo, dat waren de termen, over naar de stellingen. |
 |
| |
|
|
|
| Stelling 1. |
|
Een matching is maximaal
⇔
Er bestaat geen M-vergrotend pad. |
|
| |
|
| Let op de dubbele richting van de pijl: deze stelling geldt beide
kanten op! |
| |
Bewijs. |
| |
⇒ |
 |
| |
|
|
|
| |
|
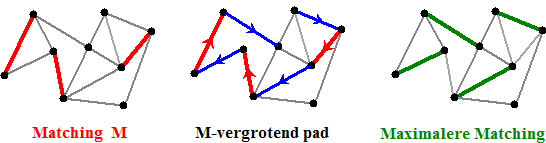
Neem van het
M-vergrotende pad gewoon de eerste, derde, vijfde, enz. lijn, dan
heb je een nieuwe matching die één groter is!
Dus als er wél een M-vergrotend pad bestaat dan is de matching niet
maximaal. Dus als de matching wel maximaal is bestaat er geen
M-vergrotend pad. |
| |
|
|
|
| |
⇐ |
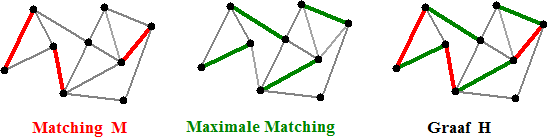
Stel dat M niet
maximaal is, en noem een maximale matching Mmax.
Bekijk nu de nieuwe graaf H die bestaat uit alle verbindingslijnen van G
(plus aanliggende knooppunten) die OF in M OF in Mmax zitten,
maar NIET in beiden. |
| |
|
|
|
| |
|
 |
| |
|
|
|
| |
|
H bestaat dan uit een
aantal componenten met om-en-om een lijn uit M en uit Mmax.
Maar omdat Mmax meer lijnen heeft dan M moet er dus een pad P
in H zijn dat begint en eindigt met een lijn uit Mmax . Dat pad P is dan
een M-vergrotend pad. |
| |
■ |
|
|
| |
|
|
|
|
Matchings in Bipartiete grafen. |
| |
|
|
|
Stel dat V een
deelverzameling is van de knooppunten van een graaf G. Dan
definiëren we de buurverzameling
B(V) als alle knooppunten van G die grenzen aan knooppunten van
V.
Stel nu dat G een bipartiete graaf is met de twee verzamelingen
knooppunten X en Y zodat elke verbindingslijn tussen een punt van X en
een punt van Y loopt.
Dan geldt: |
| |
|
|
|
| Stelling
2. |
|
Er is een matching met elk knooppunt van X erin
⇔
B(V)
≥ V
voor elke V uit X. |
|
| |
|
Dit is trouwens de "stelling van
Hall".
Let weer op de dubbele pijl! |
| |
|
| |
Bewijs. |
| |
⇒ |
Stel dat er een
matching is die elke knoop van X bevat.
Kies dan een deelverzameling V van X.
De buren van de knopen van V zijn dan in ieder geval evenveel knopen uit
Y, want elke knoop van V is verbonden aan minstens één knoop van Y. Dus
is B(V) ≥
V |
| |
|
|
|
| |
⇐ |
uit het ongerijmde:
Stel dat elke deelverzameling uit X meer buren heeft dan de verzameling
zelf groot is. Stel verder dat er géén matching bestaat waar alle
knooppunten van X in zitten.
We zullen nu proberen op een tegenstrijdigheid uit te komen....
Laat Mmax een maximale matching van G zijn. Dan is er volgens
onze aanname dus een knooppunt K in X dat niet in Mmax zit.
Bekijk nu alle Mmax-alternerende routes vanaf knooppunt K.
Dan kan er op zo'n route niet NOG een knooppunt van X voorkomen dat niet
in Mmax zit, want dan zou er een Mmax-vergrotend
pad zijn en dat kan niet volgens stelling 1 hierboven. Kortom: K
is het enige knooppunt van alle alternerende routes dat NIET in Mmax
zit. |
| |
|
|
|
| |
|
 |
| |
|
|
|
| |
|
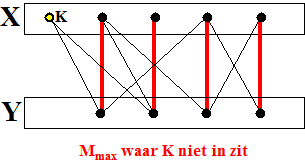
Als je nu kijkt naar
het aantal Y-knooppunten op die alternerende routes en het aantal
X-knooppunten dan vinden we de gezochte tegenstrijdigheid!
• Het aantal Y-knooppunten is eentje minder dan het aantal
X-knooppunten (want K zelf is er nog)
• Maar het aantal buren van de X-knooppunten is gelijk aan het
aantal Y-knooppunten.
• Dus is het aantal buren van de X-knooppunten eentje minder dan
het aantal X-knooppunten.
Dat is in strijd met onze aanname aan het begin. Gelukkig maar! |
| |
■ |
|
|
| |
|
|
|
| Stelling
3: De bruiloftsstelling. |
| |
|
|
|
"Elke k-reguliere bipartiete graaf heeft een
perfecte matching". |
|
| |
|
Waarom de
bruiloftsstelling?
Nou kijk: stel dat ieder meisje in een dorpje precies k jongens
kent waarmee ze zou willen trouwen en elke jongen kent ook precies k
meisjes waarmee hij zou willen trouwen. Dan zegt deze stelling dat alle
jongens en meisjes dan zouden kunnen trouwen!! |
 |
| |
Bewijs:
Als de graaf k-regulier is, dan zijn er evenveel X als Y
knooppunten (immers het aantal verbindingswegen is k
• X en ook k • Y).
Als V nu een willekeurige deelverzameling van knopen uit X is, dan is
het aantal buren B(V) van V groter of gelijk aan het aantal knopen in V
zelf (er zijn kV verbindingen vanaf V en omdat er bij elke
buur maximaal k lijnen kunnen aankomen zijn er minstens evenveel
buren).
Volgens stelling 2 is er nu een matching te vinden met elk knooppunt van
X erin.
Maar omdat er evenveel Y als X zijn moet dus ook wel elk knooppunt van Y
daarin zitten. Kortom: er is een perfecte matching. Iedereen kan
trouwen!! |
| |
■ |
|
|
| |
|
|
|
|
Toepassing: Taken toekennen
aan Werkers. |
| |
|
|
|
Stel er is een
fabriek met een aantal werkers W1, W2, ....Wn
en evenveel taken T1, T2, ....Tn
die gedaan moeten worden. Elke werker is echter niet geschikt voor
alle taken; iedere werker heeft zijn eigen specialisme(n) en kan slechts
een aantal taken doen.
De vraag is dan natuurlijk: Kunnen we alle taken onder alle
werkers verdelen?
Deze situatie kun je natuurlijk voorstellen als een bipartiete graaf van
de Werkers naar de Taken waarbij een verbindingslijn aangeeft dat de
betreffende werker de taak kan doen. De vraag is dan "Is er een
perfecte matching?"
We zullen hier een recept (oké: algoritme, dat klinkt beter)
bekijken om te ontdekken of er zo'n perfecte matching is, en ook (als er
inderdaad zo'n matching is) om zo'n matching daadwerkelijk te vinden.
Basisrecept:
1. Begin met een willekeurige matching M.
2. Kies een knooppunt K uit X dat nog niet in M
voorkomt (als dat er niet is ben je klaar).
3. Maak met deze K een M-vergrotend pad. Als dat pad niet te
vinden is, dan is er geen perfecte matching te maken.
4. De eerste, derde, vijfde enz verbindingslijnen van
dat pad geven een nieuwe matching. Ga daarmee weer naar 2.
Ziet er erg simpel uit, vind je niet? De moeilijkheid zit hem
natuurlijk in stap 4: daar staat wel luchtigjes "Maak een
M-vergrotend pad", maar ja, hoe doe je dat? En lukt dat wel
altijd??
Hoe maak je een M-vergrotend pad?
Begin bij K, en ga nu als volgt een boom tekenen:
We bekijken twee verzamelingen knooppunten: V is de verzameling
van knooppunten in X en W een verzameling van knooppunten in Y. In de
figuur hieronder zijn de knopen van V geel gemaakt en die van W
groen.
In het begin kies je één knoop K voor V, en is W nog leeg. Kies voor die
K een knoop die nog niet in de matching M zit (als die er niet is, dan
zijn we klaar en hebben we een perfecte matching!)
Nu gaan we V en W als volgt uitbreiden:
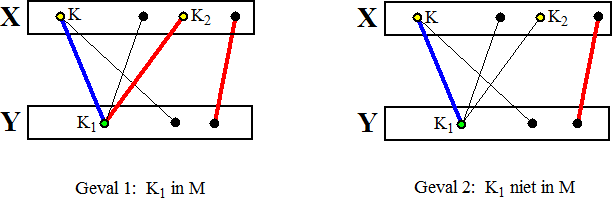
Kies een willekeurige buur K1 van K (hieronder de
blauwe lijn)
Nu zijn er twee mogelijkheden: K1 zit in M of K1
zit niet in M: |
| |
|
|
|
|
 |
| |
|
|
|
Als K1
niet in M zit zijn we klaar, want dan kunnen we M uitbreiden met route
KK1. Dan beginnen we weer helemaal opnieuw bij stap 2
van het basisrecept hierboven.
Als K1 wel in M zit, dan is er dus een M-route K1K2.
We voegen K1 toe aan verzameling W en K2 aan
verzameling V.
Kijk nu eerst of er nog nieuwe buren van V te vinden zijn
(dus buren van gele knooppunten die nog niet groen zijn). Als dat
niet zo is, dan kunnen we wel stoppen want dan hebben we een verzameling
van knooppunten V waarvan de verzameling van buren W één kleiner is
(tijdens dit hele proces is W steeds één kleiner dan V). Stelling 2
hierboven zegt dat er dan geen perfecte matching te vinden is.
Als er nog wel nieuwe buren te vinden zijn, dan gaan we weer een
willekeurige nieuwe buur van een knoop van V kiezen, en begint het hele
verhaal opnieuw.
Op deze manier komen we OF bij een perfecte matching uit OF we
ontdekken dat er geen perfecte matching bestaat.
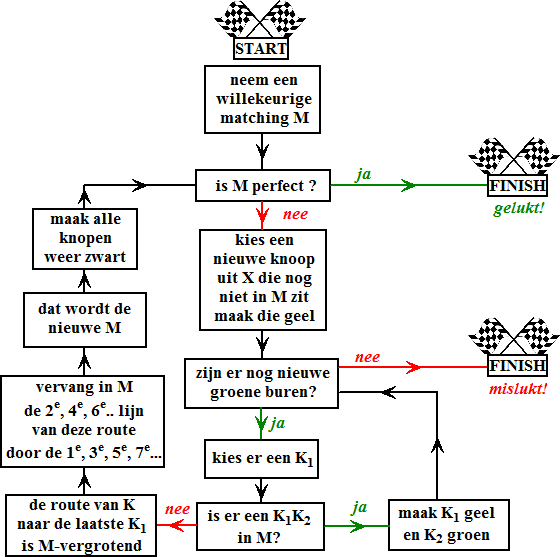
Wacht, dit toch wel wat verwarrende verhaal is misschien duidelijker in
een stroomdiagram: |
| |
|
|
|
|
 |
| |
|
|
|
| Twee voorbeelden van
het systeem in werking: |
| |
|
|
|
|
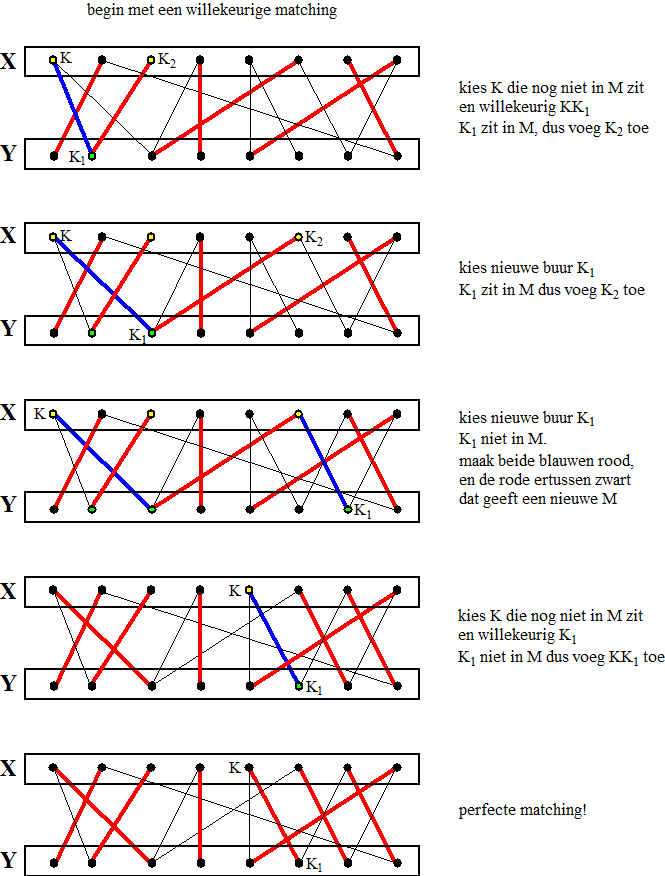
VOORBEELD 1. |
| |
|
|
|
|
 |
| |
|
|
|
|
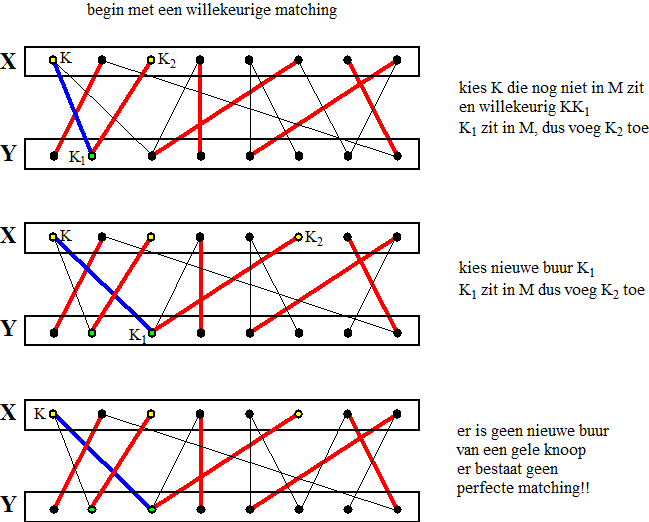
VOORBEELD 2. |
| |
|
|
|
|
 |
| |
|
|
|
| |
Merk nog even op dat
dit vastloopt omdat we een verzameling knooppunten V uit X vinden V = {X1,
X3, X6} waarvan de verzameling buren in W
uit Y kleiner is W = {Y2, Y3}.
Die twee verzamelingen zijn voor de volgende les van belang!! |
| |
|
|
|
|
OPGAVEN |
| |
|
|
|
| 1. |
Uit een schaakbord
worden het veld linksboven en het veld rechtsonder weggelaten.
Toon aan dat de overgebleven velden niet bedekt kunnen worden met
rechthoekjes van 2 bij 1. |
| |
|
|
|
| |
|
|
 |
| |
|
|
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|