| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Projecties en Spiegelingen |
| |
|
|
|
Er zijn nog twee
bewerkingen die we uit kunnen voeren op een vector, en dat zijn
projecties en spiegelingen. Daarbij gaat het alleen om, projecties op
lijnen door de oorsprong en spiegelingen in lijnen door de oorsprong.
Als lijnen niet door de oorsprong gaan, dan zijn de afbeeldingen niet
lineair.
Ga zelf maar even snel na dat dan niet geldt M(λv) =
λM(v)
Om de matrix die bij zo'n projectie of spiegeling hoort te vinden gaan
we gebruik maken van de beelden van de basisvectoren (zoals we in de
vorige les al deden) |
| |
|
|
|
|
1. Projectie op de
lijn y = ax. |
| |
|
|
|
Oké, de jacht is
geopend op het beeld van punt (1, 0) bij spiegeling in de lijn
y = ax En op het beeld van (0, 1) natuurlijk; als we ze
beiden hebben opgespoord hebben we direct matrix M gevonden.
Begin met het punt (1, 0)
Maak een lijn m loodrecht op y = ax die
door (1, 0) gaat.
De helling daarvan is -1/a dus
het is de lijn y = -1/a • x
+ 1/a
Snijden met de lijn y = ax geeft -1/a
• x + 1/a = ax
Vermenigvuldig met a: -x + 1 = a2x
Dat geeft x = 1/(1 + a˛)
en dan is y = a/(1 + a˛)
Doe dan hetzelfde met punt (0, 1) :
De loodrechte lijn wordt y = -1/a
• x + 1
Het snijpunt wordt x = a/(1
+ a˛) en y =
a˛/(1 + a˛) |
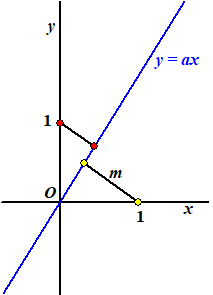 |
| We hebben nu de beide
beelden van de basisvectoren, dus is de matrix bekend: |
| |
|
|
|
|
|
| |
|
|
|
| trouwens, voor wie er
meer meetkundig aangelegd is, kun je deze beide beelden ook makkelijk
met gelijkvormige driehoeken afleiden. Misschien nog wel
makkelijker..... Als je dat graag wilt zien, kijk dan bij de verdieping
hiernaast. |
| |
|
|
 |
|
2. Spiegeling in de
lijn y = ax. |
| |
|
|
|
Onze uitgebreide
projectie-kennis kunnen we nu natuurlijk makkelijk gebruiken om te
spiegelen in de lijn y = ax. Immers dan gaan we
vanaf (1, 0) naar het projectiepunt ( 1/(1 + a˛)
, a/(1 + a˛))
en dan "nog een keer zoveel verder".
Laten we dat maar met vectoren opschrijven, dat lijkt me wel zo
veilig.
Noem (1, 0) = P en het projectiepunt P' en het spiegelpunt P'',
dan geldt: |
|
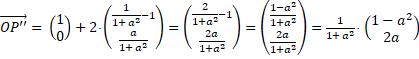 |
| En hetzelfde met
(0, 1) = Q en het projectiepunt Q' en het spiegelpunt Q''
geeft dan: |
|
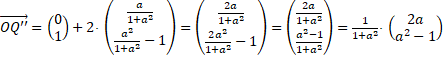 |
| We hebben nu de beide
beelden van de basisvectoren, dus is de matrix bekend: |
| |
|
|
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
|
OPGAVEN |
| |
|
|
|
| |
|
|
|
| 1. |
Het is
logisch dat spiegelen in y = ax gelijk is aan zijn
eigen inverse.
Laat zien dat de matrix van een spiegeling in een lijn y
= ax gelijk is aan zijn eigen inverse. |
| |
|
|
|
| 2. |
Het is
logisch dat projectie op de lijn y = ax voor
steeds grotere a nadert naar projectie op de y-as.
Laat zien dat dat klopt met de gegeven matrix voor projectie op
y = ax. |
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
|
| |
|
|
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|