| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
|
Alle remmen los...... |
| |
|
|
|
| 1. |
Paashaas met problemen.
Het inpakken van alle
eitjes blijkt voor de paashaas een enorm karwei. Daarom besluit
hij te gaan automatiseren. Hij gaat een inpakmachine kopen. Hij vraagt
bij de machinefabriek een offerte aan, en het blijkt dat de fabriek maar
liefst 7 modellen kan leveren. Het verschil in prijs zit hem vooral in
de nauwkeurigheid van inpakken.
De paashaas pakt de eieren in in doosjes waar ideaal gesproken 200 gram
in zit, maar het gewicht dat de machine afweegt blijkt normaal verdeeld.
De offerte levert deze tabel: |
| |
|
|
|
| |
| machine |
prijs p |
standaarddeviatie
σ
in gram |
A
B
C
D
E
F
G |
€
15000
€ 6229
€ 4948
€ 4139
€ 3577
€ 2842
€ 2377 |
1,0
3,0
4,0
5,0
6,0
8,0
10,0 |
|
| |
|
|
|
| |
Neem aan dat de
gegeven standaarddeviaties onafhankelijk zijn van het gemiddelde
gewicht.
De volgende formule is van toepassing op deze tabel: p
(σ) = 15000 •
σ-0,8
|
| |
|
|
|
| |
a. |
Zet deze gegevens uit
op dubbellogaritmisch papier en toon daarmee aan dat p inderdaad
evenredig is met
σ-0,8 |
| |
|
|
|
| |
De keuringsdienst van
Waren eist dat slechts 10% van de doosjes met eitjes minder dan het
aangegeven gewicht mag bevatten. Daaruit volgt dat voor het gewicht (G
in gram) waarop de machine moet worden afgesteld bij benadering de
volgende formule geldt: G = 200 + 1,3σ. |
| |
|
|
|
| |
b. |
Toon deze formule aan. |
|
| |
|
|
|
| |
De paashaas verwacht
met zijn machine 1.000.000 dozen te kunnen vullen. Neem aan dat de
kosten van een doos alleen bestaan uit inpakkosten (afschrijving van de
machine) en materiaalkosten (kosten van de eitjes zelf).
De kosten van de eitjes zijn €1,50
per kg.
Voor de totale kosten over 1.000.000 dozen geldt dan: K =
300000 + 15000σ -0,8 + 1950σ |
| |
|
|
|
| |
c. |
Toon deze formule aan. |
|
| |
|
|
|
| |
d. |
Bereken algebraïsch
voor welke standaarddeviatie de totale kosten minimaal zullen zijn, dus
welke machine de paashaas het best kan aanschaffen. |
| |
|
|
|
| 2. |
Leraar in nood!
De eindexamenklas van een middelbare school besluit op de laatste
schooldag gezellig met 'n allen te gaan wadlopen. Het wordt een mooie
tocht van zo'n 2 uur die zonder incidenten verloopt. Echter bij aankomst
om precies 19:05 uur blijkt tot ieders verbazing de wiskundeleraar te
ontbreken. De man is achterop geraakt en vast komen te zitten in de
zuigende modder.
Uiteraard kent de leraar de getijdenkrommen ter plekke uit zijn hoofd,
en hij weet dat voor deze plaats op deze datum geldt: |
| |
h(t) = 2 + 2sin1/2(t
- 8) |
| |
|
|
|
| |
Daarbij is t
de tijd in uren met t = 0 op 00:00 vandaag, en h de
waterhoogte op de plaats waar de man vastzit in meter. De leraar is 1,90
meter lang en zijn mond bevindt zich op hoogte 1,77 m boven de modder. |
| |
|
|
|
| |
a. |
Bereken algebraïsch
tot hoe laat de man adem zal kunnen halen. |
| |
|
|
|
| |
b. |
Hoe snel stijgt het
water op dit moment? Geef je antwoord in cm/min. |
| |
|
|
|
| |
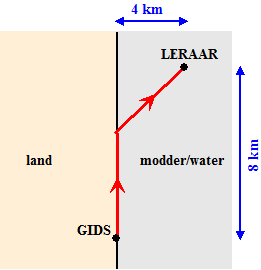
De situatie is als
hiernaast.
De gids van de tocht besluit tot een reddingsactie. Hij gaat zo snel
mogelijk naar de leraar lopen. Over het land loopt hij met 12 kn/uur, en
door de modder slechts met 6 km/uur. Hij besluit te lopen zoals
hiernaast geschetst.
De gids besluit om x km over land langs het water te lopen en
daarna rechtstreeks door de modder naar de leraar.
Voor de totale tijd die hij daarvoor nodig heeft geldt:
T = 1/12x
+ 1/6√(x2
- 16x + 80) |
 |
| |
|
|
| |
c. |
Toon aan dat deze formule geldt. |
| |
|
|
|
| |
d. |
Bereken algebraïsch
voor welke x de totale reistijd minimaal is. |
| |
|
|
|
| |
e. |
Hoelang mag de gids
over vraag c) en d) doen als de leraar dit moet overleven? |
| |
|
|
|
| 3. |
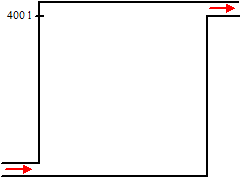
Een vloeistof wordt
bewaard in een vat. Na het gebruik is het vat nooit helemaal leeg. Om
het weer te kunnen gebruiken moet het worden schoongespoeld. Zie de
figuur hiernaast.
Via een pijp linksonder wordt spoelmiddel in het vat gepompt. Het
restant vloeistof vermengd zich met het spoelmiddel.
Na een tijdje is het vat vol, en stroomt aan de bovenkant het mengsel
van spoelmiddel en vloeistof er uit.
Het vat hiernaast heeft een inhoud van 400 liter. In het gein zit er nog
0,8 liter vloeistof in, met daarin 20000 mg van een chemische stof. Het
spoelmiddel wordt met 25 liter per minuut het vat ingepompt.
De concentratie C is de hoeveelheid chemische stof per liter
vloeistof. Tijdens het vollopen van het vat geldt de volgende formule
(daarin is t de tijd in minuten): |
 |
| |
|
|
|
| |
|
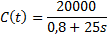 |
|
| |
|
|
|
| |
a. |
Leg uit waarom deze
formule juist is. |
| |
|
|
|
| |
b. |
Bereken algebraïsch
wanneer de concentratie gelijk zal zijn aan 60 mg/liter |
| |
|
|
|
| |
c. |
Welke horizontale
asymptoot heeft de grafiek van C? Wat stelt dit in praktijk voor? |
| |
|
|
|
| |
Als het vat vol is
blijft er evenveel onder instromen als boven uitstromen. De concentratie
van de stof neemt nu exponentieel af.
In de volgende tabel zie je de concentratie C voor enkele waarden van
t |
| |
|
|
|
| |
| t (minuten) |
16 |
20 |
24 |
28 |
| C (mg/liter) |
50,00 |
38,94 |
30,32 |
23,61 |
|
| |
|
|
|
| |
d. |
Bereken de
groeifactor van dit exponentiële proces.
Vergelijk deze gevonden groeifactor met de factor die je zou krijgen als
je aan zou nemen dat alle vloeistof zich steeds direct geheel
gelijkmatig over alle spoelmiddel verdeelt. |
| |
|
|
|
| 4. |
Hiernaast
zie je een sneeuwpop die ondersteund wordt door een gelijkzijdige
driehoek, zodat hij niet omvalt.
Als we de oorsprong midden onder kiezen, zoals in de figuur aangegeven,
dan is de sneeuwpop wiskundig voor te stellen als twee cirkels met
vergelijkingen :
x2 + (y - 30)2 = 900 en x2
+ (y - 75)2 = 225
De driehoek is zó onder de sneeuwpop geschoven dat de zijde ervan de
cirkel raakt.
Het raakpunt is het punt R = (15√3,
15)
|
 |
| |
a. |
Toon aan
dat de driehoek de cirkel inderdaad raakt in punt R.
|
| |
De top van
de driehoek ligt precies op de hoogte van het middelpunt van de onderste
cirkel.
Dan is het zwaartepunt van de driehoek ZD = (20√3,
10) |
| |
|
|
|
| |
b. |
Toon dat
aan. |
| |
|
|
|
| |
c. |
Bereken in
twee decimalen nauwkeurig de plaats het zwaartepunt van de beide cirkels
en de driehoek samen, als je ervan uitgaat dat ze een even grote
dichtheid hebben |
| |
|
|
|
| |
Er zijn
twee lijnen te tekenen die beide cirkels raken, en de x-as
snijden. |
| |
|
|
|
| |
d. |
Geef
vergelijkingen van die lijnen. |
| |
|
|
|
| |
|
|
 |
|
© h.hofstede (h.hofstede@hogeland.nl)
|