Polya's paradox

© h.hofstede (h.hofstede@hogeland.nl)

Polya's Paradox.

Er is iets vreemds met sommige inductiebewijzen aan de hand; soms is het niet mogelijk een bepaalde bewering met inductie te bewijzen, maar kun je wél een nog veel sterkere bewering bewijzen! Neem het volgende voorbeeld.
Stel dat we willen bewijzen:

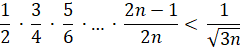Als je dat met inductie probeert zou je aannemen dat de stelling geldt voor n en dan proberen te bewijzen voor n + 1. Dat geeft dan:

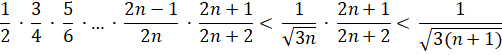Waarbij je het laatste kleiner-dan teken nog moeten bewijzen. Maar dat lukt niet!
Als je alles kwadrateert (mag want het is toch allemaal positief), en daarna haakjes wegwerkt en alles naar één kant brengt, dan blijft over 3n + 3 < 0.
En dat is duidelijk niet waar.

Maar zie wat er gebeurt als we onze voorwaarde nog strenger maken:

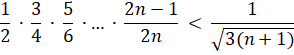Nu is het opeens wél met inductie te bewijzen. Precies dezelfde procedure als hierboven levert nu op
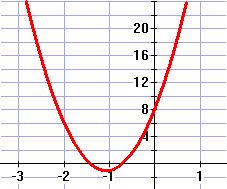
8n² + 17n + 8 > 0 En dat is voor n > 0 inderdaad altijd het geval, zoals je wel aan de parabool hiernaast kunt zien.

Nu hebben we dus een strenger geval bewezen, dus ook het oorspronkelijke geval. Maar het eerste lukte niet met inductie en dit tweede wél.

Vreemd hè?

Hier zijn er nog een paar:

OPGAVEN

Stelling:

Voeg een term ¹/_(n_{+ 1)²} toe en laat zien dat in dat geval de ongelijkheid nooit valt aan te tonen.

Bekijk nu de strengere ongelijkheid:

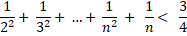Laat zien dat het toevoegen van een term voor n + 1 nu een ongelijkheid geeft die wél is aan te tonen.

Stelling:

n! kan geschreven worden als som van n delers van zichzelf.

Een inductiebewijs zou zó beginnen:
• 1! kan geschreven worden als 1.
• Stel dat geldt n! = d₁ + d₂ + ... d_n waarin de d's allemaal delers van n! zijn (er mogen dezelfden bijzitten)
• Hoe zit het dan met (n + 1)!

Vermenigvuldig de vergelijking daarom met n + 1
Waarom kun je hier nu de stelling nog niet mee bewijzen?

Zorg dat de vergelijking (n + 1) termen krijgt, en ga na of al die termen inderdaad delers van (n + 1)! zijn
Welke extra strengere voorwaarde maakt het mogelijk de stelling te bewijzen?