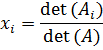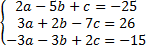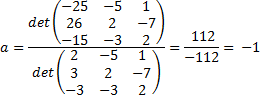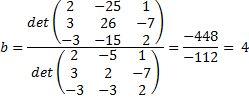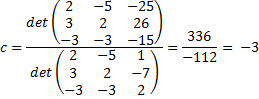regel van Cramer

© h.hofstede (h.hofstede@hogeland.nl)

De regel van Cramer.

Gabriël Cramer hiernaast verzon een regel om een stelsel direct op te lossen zonder eerst de inverse matrix te hoeven berekenen en ook zonder schoon te vegen.

Leuke bijkomstigheid: je hoeft niet eens de hele oplossing in één keer te berekenen, maar je kunt alle afzonderlijke variabelen apart berekenen. Welke je maar wilt....

Het werkt als volgt.
Schrijf het stelsel vergelijkingen in de vorm:

A • x = b

Waarin A de coëfficiëntenmatrix is, en x de kolomvector met de variabelen x₁, x₂, x₃, ... die je wilt berekenen.
Dan is de oplossing voor variabele x_i :

Daarin is A_ide matrix die je krijgt door in de coëfficiëntenmatrix A de i^de kolom te vervangen door b.

voorbeeld.

Neem het volgende stelsel van drie vergelijkingen:

Dan geldt in één keer:

Je ziet dat daar in de teller steeds een andere kolom door b is vervangen. Niet zomaar eentje natuurlijk: precies de kolom van de variabele die je wilt berekenen is vervangen!!!
Nou, dat is alles, meer kan ik er ook niet van maken..... behalve dan natuurlijk dat dit alleen maar geldt als er één oplossing is, dus als de noemer (de determinant van de coëfficiëntenmatrix dus) niet nul is, maar dat had je zelf ook al wel verzonnen natuurlijk. Sorry voor de belediging.