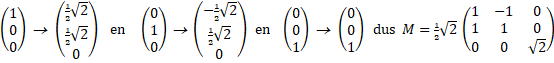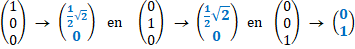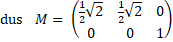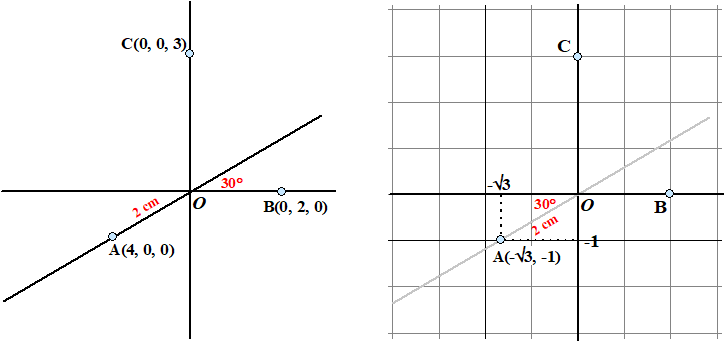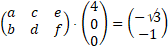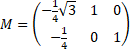|
|||||||||||||||||||||||||||||||
| Driedimensionale Lineaire Afbeeldingen | |||||||||||||||||||||||||||||||
| Ook in
ℝ3 kun je natuurlijk
vermenigvuldigingen, Spiegelingen, Rotaties en Projecties uitvoeren. De (kolom)vectoren hebben dan 3 kentallen en de matrices zijn 3 ◊ 3. Het is weer zo dat de beelden van de basisvectoren precies de kolommen van de matrix zijn. Niks nieuws onder de zon. Voorbeeld. Geef de matrix voor draaiing over 45° om de z-as. Bekijk de drie beelden van de basisvectoren: |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Afbeeldingen van ℝ3 naar ℝ2 | |||||||||||||||||||||||||||||||
| Dat zijn dus
projecties! De ruimte (ℝ3)wordt geprojecteerd op een plat vlak (ℝ2). In dit geval zal de matrix M een 2 ◊ 3 matrix zijn (2 rijen en 3 kolommen) anders kan het beeld van een 3 ◊ 1 vector nooit een 2 ◊ 1 vector worden. Je moet wel even goed definiŽren wat de basisvectoren van je projectievlak zijn. |
|||||||||||||||||||||||||||||||
|
Voorbeeld. Geef
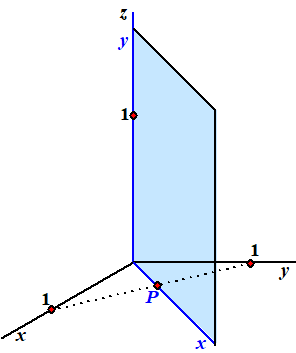
de matrix voor projectie op het vlak x = y Zie de figuur hiernaast. De hele ruimte wordt afgebeeld op het blauwe vlak. Stel dat we de x-as en de y-as in het blauwe vlak zo kiezen als hiernaast. Dan worden de x- en y basisvectoren beiden afgebeeld op punt P, en dat punt heeft met de nieuwe (blauwe) assen de coŲrdinaten (1/2√2, 0) Dan geldt voor de basisvectoren: |
|
||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Nou je deze matrix M eenmaal hebt, kun je vliegensvlug uitrekenen dat bijv het punt (1, 2, 3) wordt afgebeeld op het nieuwe punt (3/2√2, 3). | |||||||||||||||||||||||||||||||
| Deze techniek wordt
natuurlijk erg vaak gebruikt in computerspellen waarin je een 3D-wereld
wilt afbeelden op een plat vlak, namelijk op je computerscherm. Maar je kunt als projectievlak natuurlijk ook gewoon het papier van je schrift nemen: |
|||||||||||||||||||||||||||||||
| Links zie je een
ruimtelijk assenstelsel in parallelprojectie (met de x-as onder
een hoek van 30 en verkortingsfactor 1/2) Daarin zijn de punten (A, 4, 0, 0) en B(0, 2, 0) en C(0, 0, 3) getekend. |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Rechts is daar een
"gewoon" plat assenstelsel overheen gelegd met dezelfde oorsprong
(die oorspronkelijke x-as is er dus niet meer) In dat assenstelsel is A = (-√3, -1) en B = (2, 0) en C = (0, 3) Dus moet gelden: |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Dus is a
= -1/4√3 en
b = -1/4 Op dezelfde manier volgt uit de beelden van B en C dat c = 1 en d = 0 en e = 0 en f = 1 De matrix die deze projectie op het vlak van ons papier beschrijft is dus: |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| En voor andere soorten projecties (bijv. de ingenieursprojectie, scheve projectie of isometrische projectie) kun je ook makkelijk zo'n matrix opstellen. | |||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||||||||||||||||||||||||||||