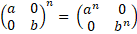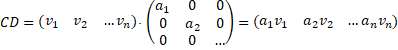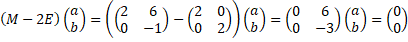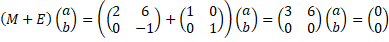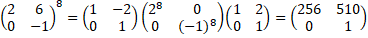© h.hofstede (h.hofstede@hogeland.nl)

Een matrix diagonaliseren.
       
In het algemeen is het eigenlijk best veel werk om matrices met elkaar te vermenigvuldigen. En helemaal om matrices tot-de-macht te nemen. Terwijl je dat best vaak nodig hebt. Denk aan een overgangsmatrix (deze les) van een systeem waarvan je het gedrag op de langere duur wilt voorspellen; dan moet je Mn  berekenen.

Nou is er één soort matrices waarvan je wel makkelijk Mn  kunt berekenen, en dat zijn matrices met alleen maar getallen op de hoofddiagonaal. Kijk maar:

       
Zo'n matrix met alleen maar getallen op de hoofddiagonaal noemen we een diagonaalmatrix.
Het zou voor vermenigvuldigingen dus erg handig zijn als we een matrix kunnen veranderen in een diagonaalmatrix.

Je raadt het al:  DAT KAN!

Stelling.
Als M een matrix is, en D een diagonaalmatrix met diagonaalgetallen a1, a2, .... en C een matrix waarvan de kolommen  de vectoren v1, v2, .... zijn.  Dan geldt  MC = CD dan en slechts dan als de ai's de eigenwaarden van M zijn, en de vi's de bijbehorende eigenvectoren.
       
Bewijs.
  ⇒

 

  Dus Mv1 = a1v1 en  Mv2 = a2v2  enz.
Dat is precies de definitie van eigenwaarden ai en eigenvectoren vi
     
⇐ Het bewijs de andere kant op gaat precies zo.
q.e.d.    
       
Stel nou dat matrix C een inverse C-1  heeft.
Dan kun je schrijven:
MC = CD
C-1MC = C-1CD = D
Dus matrix C kun je gebruiken om van matrix M een diagonaalmatrix D te maken!  M noemen we dan diagonaliseerbaar, en we zeggen dat C matrix M diagonaliseert.

Is elke vierkante matrix diagonaliseerbaar?

Het antwoord daarop staat eigenlijk al hierboven:  JA, mits de matrix C van de eigenvectoren een inverse heeft.
En dat is zo als de eigenvectoren een onafhankelijk stelsel vormen, want dan is de determinant van de matrix niet nul.
Kortom; wat kan er misgaan?
  • Als een matrix geen eigenwaarden heeft, dan is hij ook niet diagonaliseerbaar.
  • Als een matrix één eigenwaarde heeft zijn er twee mogelijkheden:
        1.  die ene λ geeft twee onafhankelijke eigenvectoren; in dat geval is M diagonaliseerbaar
    2.  die ene λ geeft één eigenvector; in dat geval is M niet diagonaliseerbaar
  • Als een matrix twee verschillende eigenwaarden heeft is hij diagonaliseerbaar, behalve als de twee eigenvectoren op dezelfde lijn liggen (want dan zijn ze niet onafhankelijk).
       
Voorbeeld.
 

  | M - λE | = (2 - λ)(-1 - λ)  = 0  geeft eigenwaarden  λ1 = 2  en   λ2 = -1
  eerste eigenwaarde:
 

  Dat geeft  a = 1  en  b = 0
  tweede eigenwaarde:
 

  Dat geeft  a = -2b
 

  (Ga dat zelf na door de determinant te berekenen of door schoon te vegen)
 

  Inderdaad een diagonaalmatrix.
       
Wat kunnen we ermee?
       
C-1MC = D
vermenigvuldig beide zijden links met C:  dat geeft  CC-1MC = CD  dus  MC = CD  (hadden we boven ook al)
vermenigvuldig beide zijden  rechts met C-1;  dat geeft  MCC-1 = CDC-1  dus  M = CDC-1
       

M = CDC-1
       
Nu kun je supersnel Mn  uitrekenen, kijk maar:

Mn
= MMMMMMMM...
= (CDC-1) (CDC-1)(CDC-1)(CDC-1)(CDC-1)(CDC-1)(CDC-1)(CDC-1)....
=  CD(C-1C)D(C-1C)D(C-1C)D(C-1C)D(C-1C)D(C-1C)D(C-1C)D(C-1....
=  CDDDDDDDD...C-1
= CDnC-1

En omdat die D een diagonaalmatrix is, kun je Dn berekenen door gewoon alle elementen op de diagonaal (de eigenwaarden van M trouwens) tot de macht n te nemen.

Met bovenstaand voorbeeld:

Controleer maar met je GR dat het klopt.  Maar ook M200  geeft niet meer rekenwerk!!!
       
Gevolgen voor de determinant.

In een eerdere les zagen we al dat voor de determinant van inverteerbare matrices geldt:  |A • B| = |A| • |B|
Neem nu B = A-1
Dan geeft dat   |A • A-1| = |A| • |A-1| = 1  want A • A-1 = I;  de eenheidsmatrix
Als je matrix M nou kunt diagonaliseren, dan staat er:
M = C • D • C-1  dus  |M| = |C • D • C-1|= |C| •  |D| •  |C-1| = |D|
En die determinant van D die kennen we;
omdat D de matrix is met de eigenwaarden op de hoofddiagonaal geldt dat | D | = λ1 • λ2 • λ3 ...
       
Voor een diagonaliseerbare matrix M geldt:
 | M | = λ1 • λ2 • λ3 ...
       
Stelling van Cayley-Hamilton.
       
Elke vierkant matrix voldoet aan zijn eigen karakteristieke vergelijking.
       
Ik hoop dat je nog weet dat de karakteristieke vergelijking er zó uitziet:    |M - λE| = 0
Dat gaf als oplossing een aantal eigenwaarden λ1, λ2, ...
(λ - λ1) (λ - λ2) ..... = 0 is het karakteristieke polynoom

Als M daar zelf aan moet voldoen, dan moet dit polynoom worden  (M - λ1E)(M - λ2E)... = 0
Laten we één zo'n factor bekijken, bijvoorbeeld de eerste:

M - λ1E
Schrijf M nu als CDC-1  (diagonaliseer matrix M).
CDC-1 - λ1E
=  CDC-1 - λ1CEC-1
=  C(D - λ1E)C-1
Maar  D - λ1E  geeft een matrix met de eerste rij alleen maar nullen (immers op de hoofddiagonaal  van D stond alleen een λ1).

Zo geeft  M - λ2E  een matrix met op de tweede rij alleen maar nullen.
Zo geeft  M - λ3E  een matrix met op de derde rij alleen maar nullen.
Je snapt het idee waarschijnlijk wel:   als je al die matrices met elkaar vermenigvuldigt komt er nul uit.
Dus voldoet M aan zijn eigen karakteristieke vergelijking.

Hé, grappig:  dat geeft een manier om van een 3×3 matrix met eigenwaarden a, b, c de inverse te vinden, kijk maar:
(M - aE)(M - bE)(M - cE) = 0  (Cayley en Hamilton zeggen dat; die 0 is eigenlijk de "nulmatrix")
(M - aE)(M2 - (b + c)M + bcE = 0
M3 - M2(a + b + c) + M(ab + bc + ac) - abcE = 0
M3 - M2(a + b + c) + M(ab + bc + ac) = abcE
Vermenigvuldig beide kanten met M-1 , en deel door abc:

       
       
   OPGAVEN
       
1.      
       
       
       
       
       
       
       
       
       
       
       
       
       
       
       
       
       
       
       
       
       
       

© h.hofstede (h.hofstede@hogeland.nl)