planaire grafen

© h.hofstede (h.hofstede@hogeland.nl)

Planaire Grafen

"Planair" betekent eigenlijk "uit het platte vlak" dus planaire grafen zijn grafen zoals in de vorige les: waarvan de knooppunten landen zouden kunnen zijn en de verbindingslijnen kunnen aangeven of ze aan elkaar grenzen of niet.

Maar dat betekent dat die verbindingslijnen elkaar niet kunnen snijden! Immers bij landen kun je op de plaats van de grens op de kaart ook de verbindingslijn tekenen, en daar kunnen/hoeven geen verbindingslijnen van andere grenzen doorheen te lopen. Die kunnen gewoon op hun eigen plaats....

Een landkaart (met de landen als knooppunten) zou je dus kunnen omschrijven als een "samenhangende planaire graaf".
Een graaf waar wél doorsnijdingen nodig zijn is dus niet-planair. Het kruisingsgetal is het minimaal benodigde aantal doorsnijdingen dat nodig is.

Laten we die samenhangende grafen zonder doorsnijdingen (dus met kruisingsgetal 0) verder onderzoeken....

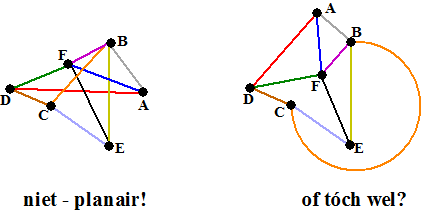
Op de eerste plaats moet je je bedenken dat plaatjes kunnen bedriegen. De graaf hier linksonder lijkt niet planair, immers de verbindingslijnen snijden elkaar. Erg vaak zelfs....
Maar als je 'em tekent zoals rechtsonder dan zie je dat hij wél planair is!!

We noemen een graaf G planair als er een met G isomorfe graaf te vinden is die planair is. Maar ja...hoe zie je aan een ingewikkelde graaf of er zo'n variant te maken is? Dat gaan we deze les onderzoeken.

Jordan-Krommen

Eerst even een heel flauw, maar toch ook wel best ingewikkeld stukje theorie.

Een Jordankromme is een kromme in het vlak die continu is, zichzelf niet snijdt, en waarvan het beginpunt gelijk is aan het eindpunt. "Ah: een LUS" zouden simpele mensen zeggen, en daar hebben ze deze keer nog gelijk in ook!

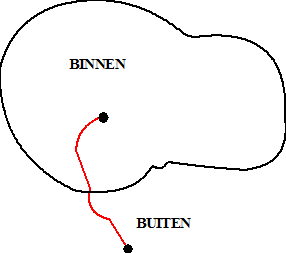
Nou verdeelt zo'n Jordankromme het vlak in twee gebieden: een BINNENgebied en een BUITENgebied. Nou is er een beroemde stelling uit de topologie die het volgende zegt:

Als je een punt uit het binnengebied verbindt met een punt uit het buitengebied, dan zal die verbindingslijn de Jordankromme altijd snijden.

Waar hebben we het eigenlijk over?
Is dit de Peuterspeelzaal? Of Sesamstraat?

Nou ja.... eigenlijk is deze stelling niet eens zo heel makkelijk te bewijzen. Ga ik hier ook niet doen,: koop maar een boek over topologie.

Door knooppunten van een graaf met elkaar te verbinden kun je natuurlijk een heleboel Jordankrommen in het vlak maken. Vandaar dat deze stelling misschien toch nog wel handig van pas zal komen. Weet je wat: we doen direct een voorbeeldje!

Stelling:

"K₅ is niet-planair".

K₅ zie je hiernaast. Het is de volledige graaf met 5 knooppunten. De stelling zegt dus dat je niet, door handig knooppunten op een andere plaats te leggen, een planaire graaf kunt maken.

het bewijs.
Stel dat het wel kan.
Noem de knooppunten k₁, k₂, k₃, k₄ en k₅.

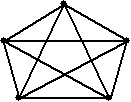Omdat K₅ een volledige graaf is, bestaat er een route k₁k₂k₃k₁ en... jawel! dat is een Jordankromme (met 3 knooppunten kan hij zichzelf immers nooit snijden).
Die verdeelt het vlak in 2 delen; het binnendeel en het buitendeel.

Stel dat k₄ in het binnendeel ligt, zoals hiernaast.

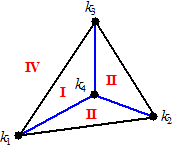
(II is bijvoorbeeld het binnengebied van k₂k₄k₃k₂)
Voor de plaats van k₅ zijn nu 4 gebieden mogelijk (deze 3 plus het buitengebied van de kromme).
Maar in elk van die vier gebieden is k₅ niet met één van de andere knooppunten te verbinden zonder de rand van dat gebied te doorsnijden. De rand van dat gebied bestaat uit een route langs 3 van de 4 andere knooppunten, en dan is k₅ niet met dat vierde punt te verbinden.
Dus dan kan K₅ niet planair zijn.

Voor k₄ in het buitengebied geldt precies zo'n redenering (doe dat zelf maar).
Dus is K₅ nooit planair te tekenen.

■

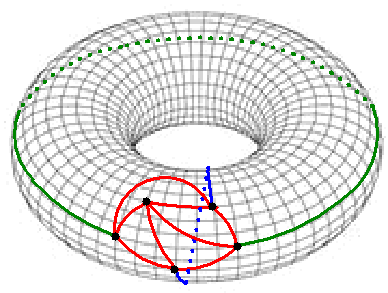
Nou ja.... nooit.... op een plat vlak dan. Op een ring is het een makkie; kijk maar:

Die blauwe en groene verbindingslijnen lopen "achterlangs" en dan kan het opeens.
Maar goed, met het tekenen van grafen op andere oppervlakken begeven we ons op het gebied van de topologie, en dat is in deze lessenserie niet de bedoeling. Dan moeten we het ook gaan hebben over grafen op een Möbius-band of op een dubbele ring, noem maar op.... Sorry....mij te ingewikkeld!

Het enige wél interessante oppervlak voor ons om een graaf op te tekenen is eigenlijk een bol (het gaat immers bij planaire grafen vaak over landkaarten). Het goede nieuws daarbij is:

Bij een bol gaat het precies zo als bij een plat vlak.

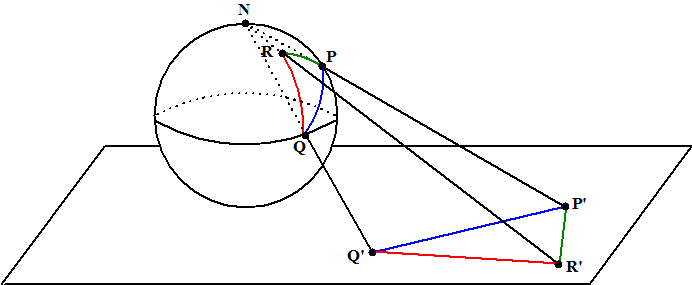
Dat dat zo is, is snel in te zien met behulp van de zogenaamde stereografische projectie:

Door een willekeurig punt P' van het vlak met de noordpool N van de bol te verbinden krijg je een punt P op de bol (het snijpunt van P'N met het boloppervlak). Op deze manier ontstaat er een één-op-één relatie tussen alle punten van het vlak en alle punten van de bol. Dus kun je grafen op het boloppervlak veranderen in grafen in het platte vlak waarbij de onderlinge ligging van de knooppunten gelijk blijft.
(Oh ja... je moet dan wel een oneindig groot vlak nemen, want punt N zélf wordt op de hele "oneindige verre" rand van het vlak afgebeeld. Je kunt er natuurlijk ook voor zorgen dat je de bol zó neerlegt dat N geen knooppunt van de graaf is).

Facetten.

Door zo'n planaire graaf wordt het platte vlak in een aantal deelgebieden verdeeld.
Die gebieden noemen we facetten.

Hiernaast zie je een voorbeeld van een graaf die het vlak in 4 facetten (f₁ tm f₄) verdeelt. f₁ is in dat geval het hele buitengebied.

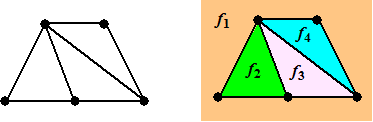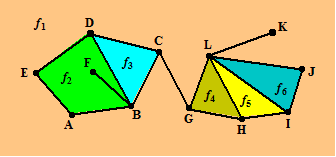
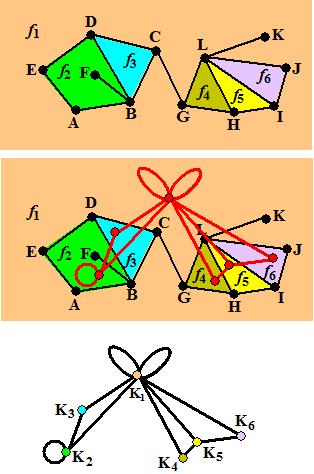
Eerst nog wat naamgeving bij een planaire graaf, aan de hand van een voorbeeldgraaf.
Deze graaf heeft 12 knooppunten (A tm L) en verdeelt het vlak in 6 facetten f.

•

Elke graaf heeft één buitengebied (in dit geval f₁)

•

Een lijnsnede is een verbindingslijn waarvoor geldt: als je hem weglaat is de graaf niet meer samenhangend. In het voorbeeld hiernaast zijn dat de lijnen BF en CG en LK

•

De grens van elk facet van de graaf is een route langs een aantal knooppunten. Daarbij wordt elke kritieke verbinding twee keer doorlopen en elke gewone verbindingslijn één keer. Bijvoorbeeld:
f₄ heeft grens GHLG.
f₂ heeft grens ABFBDEA en BF wordt twee keer doorlopen.
f₁ heeft grens EDCGLKLJIHGCBAE.

•

We noemen een facet samenvallend met alle knooppunten en verbindingslijnen van zijn grens.
In het voorbeeld valt f₃ dus samen met B, BC, C, CD, D en DB.
Elke verbindingslijn heeft dan twee facetten waar hij mee samenvalt, behalve de kritieke verbindingen: die hebben maar één facet waar mee ze samenvallen (BF alleen met f₂, CG en LK alleen met f₁)

•

De graad van een facet is het aantal verbindingslijnen in zijn grens (daarbij worden kritieke verbindingen dubbel geteld!)

•

Een verbindingslijn scheidt twee verschillende facetten als hij in beide grenzen voorkomt.

de Duale Graaf.

Je kunt een graaf G veranderen in een nieuwe graaf G* volgens de volgende twee regels:

1. Elk facet f van G geeft een kooppunt K van G*

2. Elke verbindingslijn in G die twee facetten scheidt geeft een nieuwe verbindingslijn in G* die de overeenkomstige knooppunten verbindt. Een verbindingslijn die niet twee facetten scheidt geeft een lus.

Die nieuwe graaf G* heet de duale graaf van G.
('t Is eigenlijk precies wat we de vorige les al deden met dat kleuren van die landkaart, maar dan allemaal wat formeler gesteld). Hiernaast zie je hoe de bovenstaande graaf G verandert in zijn duale graaf G*.
Merk nog even de twee lussen bij K₁ op: ten gevolge van de kritieke verbindingen CG en LK.

Als G planair is, dan is G* dat ook!
Dat is heel eenvoudig zo te zien : Teken elk knooppunt van G* gewoon ergens in het overeenkomstige facet van G. De verbindingslijn van twee knooppunten in G* teken nu zó dat hij de overeenkomstige verbindingslijn in G precies één keer snijdt. Dan kunnen twee verbindingslijnen van G* elkaar nooit snijden, want dat zogenaamde snijpunt hoort dan ook bij twee verbindingslijnen van G en die snijden elkaar niet omdat G planair was.

Merk nog even op dat G en G* beslist niet isomorf hoeven te zijn. In het voorbeeld hierboven heeft G bijv. wel knooppunten met één verbindingslijn en G* niet.

Merk tenslotte nog op dat de duale graaf van de duale graaf weer G zelf oplevert: G** = G

Logische verbanden tussen een graaf en zijn duale graaf (die direct uit de constructiemethode volgen):

1. aantal knooppunten van G = aantal facetten van G*
2. aantal verbindingslijnen G = aantal verbindingslijnen G*
3. graad van een facet van G = graad van het bijbehorende knooppunt van G*

Hulpstelling voor straks:

De som van de graden van alle facetten van een planaire graaf
is gelijk aan het dubbele van aantal verbindingslijnen van die graaf.

Bewijs van de hulpstelling voor straks:
Noem f het aantal facetten, V het aantal verbindingslijnen en K het aantal knooppunten, dan geldt:

som van alle graden van de facetten van G = som van alle graden van de knooppunten van G* (eigenschap 3)
som van graden van knooppunten van elke graaf = 2 • aantal verbindingslijnen van de graaf (immers elke verbindingslijn levert twee graden op).
maar omdat het aantal verbindingslijnen van G en G* gelijk zijn (eigenschap 2) volgt daar direct de stelling uit.

OPGAVEN

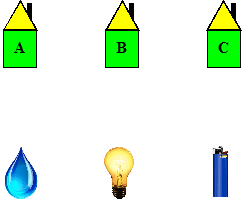
1.	Een beroemd raadsel..... Drie huisjes, A, B en C, moeten elk met water, gas en licht verbonden worden. De leidingen daarvoor komen even diep te liggen, en mogen elkaar niet kruisen. Toon aan dat dat onmogelijk is. Vertaling: Toon aan dat K_3,3 niet planair is.

2.	Een graaf heet zelf-duaal als hij isomorf is met zijn duale graaf. Toon aan dat voor een zelf-duale graaf geldt: V = 2K - 2

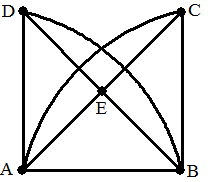
3.	Onderzoek of de graaf hieronder planair is of niet.



4.	Bepaal het kruisingsgetal van K₅