| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
 |
|
Betrouwbaarheidsinterval voor een
proportie. |
| |
|
|
|
|
De vorige les hebben
we gezien hoe je uit een meting die je in een steekproef hebt gedaan
conclusies kunt trekken die voor de hele populatie gelden.
Dat leverde bij een gemeten gemiddelde in de steekproef een
95%-betrouwbaarheidsinterval
voor de hele populatie op. Dat waren twee grenzen waarvan je met 95%
zekerheid kunt zeggen dat het werkelijke gemiddelde daartussen zal
liggen.
Een proportie in plaats van een
grootte.
In plaats van dat je als onderzoeker ergens de gemiddelde grootte van
hebt gemeten kan het natuurlijk ook zo zijn dat je een percentage hebt
gemeten.
Dan wil je uiteraard graag weten welke conclusies je dan kunt trekken
over dat percentage voor de hele populatie.
Het zal je niet verbazen dat je ook daarvoor een
95%-betrouwbaarheidsinterval kunt opstellen.
Je zou bijvoorbeeld kunnen meten hoeveel procent van de
eerstejaarsstudenten na een jaar nog thuis woont.
Stel dat je een enquÍte onder 200 eerstejaars studenten houdt waarvan er
70 nog thuis blijken te wonen.
Dat is 35%.
Dus zou je willen beweren: "Van de eerstejaarsstudenten woont 35%
nog thuis".
Maar ja.... Hoe betrouwbaar is die 35%.......?
Precies dezelfde vraag als in de vorige les: Hoe kun je een
steekproefmeting van 35% vertalen naar een populatiebewering?
Ook hiervoor is een formule voor het 95%-betrouwbaarheidsinterval
opgesteld (die je op de formulekaart kunt vinden) en dat is de volgende: |
| |
|
|
|
|
|
 |
| |
|
|
|
|
| Bedenk goed dat
hierin p de proportie is (en niet het percentage) dus dat
betekent dat je een percentage eerst door 100 moet delen voordat je deze
formule kunt gebruiken. Verder is n de steekproefgrootte |
| |
|
|
|
|
|
|
| |
|
|
|
|
| Bij de 35% studenten
uit het voorbeeld zou gelden: |
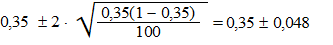 |
| Dus dat geeft een
interval [0.302 ; 0.398] ofwel tussen 30,2% en
39,8% Terugrekenen naar een
steekproefgrootte.
Het kan ook andersom: als je het
95%-betrouwbaarheidsinterval weet, dan kun je dat terugrekenen naar het
steekproefgemiddelde en de steekproefgrootte. |
|
|
Voorbeeld.
Stel dat het 95%-betrouwbaarheidsinterval van een proportie gelijk is
aan [0.461; 0.601]
Dan was het midden van de metingen gelijk aan (0,601 +
0,461)/2 = 0,531
En de breedte van het interval is 0,601 -
0.461 = 0,14, dus vanaf het midden is dat naar beide kanten 0,07
Dat betekent dat moet gelden: |
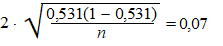 |
Voer in de GR in:
Y1 = 2 * √(0,531*(1 - 0,531)/X)
Y2 = 0,07
CALC en dan intersect geeft X = n = 203
De steekproefgrootte was dus 203 en de steekproef leverde een proportie
van 0,531 op (53,1%) |
|
| |
|
|
|
|
| |
|
|
|
OPGAVEN. |
| |
|
|
|
|
| 1. |
Een onderzoek onder
300 Vlamingen leverde op dat 76% van hen tegen de komst van nog meer
asielzoekers was.
Geef een 95%-betrouwbaarheidsinterval voor het werkelijk percentage
Vlamingen dat tegen de komst van nog meer asielzoekers was. |
| |
|
|
|
|
| 2. |
Examenopgave Havo,
Wiskunde A, 2018. Sinds de jaren tachtig meet het Trimbos-instituut
regelmatig via een enquÍte het gebruik van alcohol, drugs en tabak
in aselecte, representatieve steekproeven onder alle leerlingen van
het voortgezet onderwijs. Ook werd de leerlingen in de enquÍte
gevraagd naar hun leeftijd (in jaren), hun geslacht (jongen,
meisje), en hun schoolniveau (vmbo, havo, vwo).
Aan de enquÍte van 2015 deden 6714 leerlingen mee in
de leeftijd van 12 tot en met 16 jaar. In deze groep is onder andere
gekeken naar de lifetime-prevalentie van roken. Hieronder staat wat
dit begrip betekent: |
| |
|
|
|
|
| |
|
lifetime-prevalentie van roken = het
percentage van de leerlingen dat
rookt of ooit gerookt heeft in zijn of haar leven. |
|
| |
|
|
|
|
| |
|
lifetime-prevalentie van roken |
| steekproefomvang |
6714 |
| aantal dat rookt of ooit gerookt
heeft |
1544 |
| lifetime-prevalentie |
23% |
|
| |
|
|
|
|
| |
In de tabel zie je dat van de leerlingen in de
steekproef 23%, bijna een kwart, rookt of ooit gerookt heeft.
Bereken het
95%-betrouwbaarheidsinterval voor de lifetime-prevalentie van roken. |
| |
|
|
|
|
| 3. |
Examenopgave Havo,
Wiskunde A, 2016.
PatiŽnten die voor een behandeling enige tijd in een
ziekenhuis worden opgenomen, lopen tijdens dit verblijf het risico een
infectie te krijgen. Zoín infectie wordt een zorginfectie genoemd. Een
deel van de zorginfecties ontstaat na een operatie.In de periode 2007 tot en met 2012 is een steekproef
gehouden onder een deel van de Nederlandse ziekenhuizen. Enkele
resultaten hiervan zijn in de tabel te zien. |
| |
|
|
|
|
| |
| |
aantal |
| patiŽnten |
95299 |
| patiŽnten die een zorginfectie hebben
opgelopen |
4694 |
| geopereerde patiŽnten |
32664 |
| geopereerde patiŽnten die een zorginfectie
hebben opgelopen |
1286 |
|
| |
|
|
|
|
| |
We nemen aan dat de patiŽnten in deze ziekenhuizen
representatief zijn voor alle patiŽnten die in een Nederlands ziekenhuis
worden opgenomen.
Dan kunnen we op basis van de gegevens in de tabel schatten hoeveel
procent van alle in Nederland geopereerde patiŽnten in de genoemde
periode een zorginfectie opliep.
Bereken het 95%-betrouwbaarheidsinterval van dit
percentage. Rond de getallen in je eindantwoord af op ťťn decimaal. |
| |
|
|
|
|
| 4. |
Een onderzoek onder een aantal Vlamingen leverde op dat 76% van hen tegen de komst van nog meer
asielzoekers was.
Het 95%-betrouwbaarheidsinterval voor het werkelijk percentage was
gelijk aan [74.8 ; 77.2]
Bereken hoeveel Vlamingen aan het onderzoek meededen. |
| |
|
|
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|