netwerken

© h.hofstede (h.hofstede@hogeland.nl)

Netwerken.

Een Netwerk is een speciaal soort gerichte graaf (Digraaf). Een netwerk (vanaf nu aangegeven met N) heeft een onderliggende digraaf D, maar daar is nog iets extras mee aan de hand.
De knooppunten van een netwerk N worden onderscheiden in 3 soorten:

•

Bronnen (verzameling B)

•

Tussenliggende punten (verzameling T)

•

Putten (verzameling P)

Verder is er een functie c die aan elke verbindingslijn een getal toekent, dat we de capaciteit van die verbindingslijn noemen.

Vergelijk de situatie maar met een economisch model: de Bronnen zouden de fabrieken kunnen voorstellen, de Putten zouden dan de afzetmarkten kunnen zijn, en de verbindingslijnen zijn transportwegen waarbij de capaciteit zegt hoeveel goederen er langs elke weg vervoerd kunnen worden.
Of je kunt het ook letterlijk nemen: de bronnen maken afvalwater, de putten zijn de plaatsen waar dat geloosd moet worden, en de verbindingslijnen zijn waterleidingen, elk met een eigen capaciteit (doorsnede).

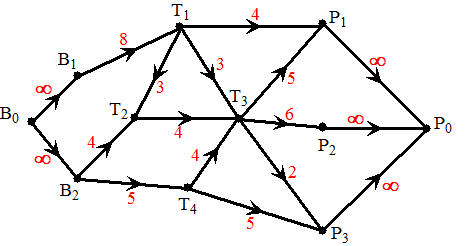
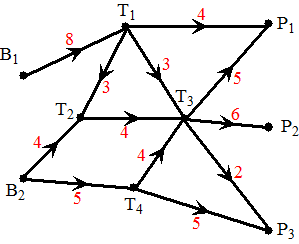
Hiernaast zie je een netwerk met 2 bronnen en 3 putten en 4 tussenliggende punten.

Merk nog even op:
- Bronnen hebben alleen uitgaande verbindingslijnen.
- Putten hebben alleen inkomende verbindingslijnen.
- Alle capaciteiten zijn positief.

opmerking: Als de verbindingslijnen beide kanten op kunnen vervoeren (zoals waterleidingen), dan kun je dat makkelijk tot stand brengen door tussen die punten twee gerichte verbindingslijnen te tekenen met dezelfde capaciteit; eentje heen en eentje terug.

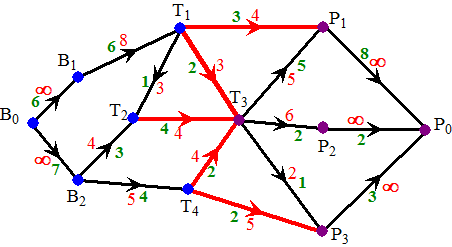
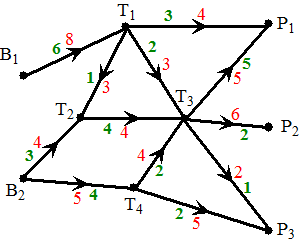
Een stroom in een netwerk is nu een functie die aan elke verbindingslijn een waarde toekent (de groene getallen in de figuur hieronder), waarbij wordt voldaan aan twee voorwaarden:

De toegekende waarden zijn allemaal hoogstens gelijk aan de capaciteit van de lijnen.

Voor tussenliggende knopen geldt: totale stroom erin = totale stroom eruit. Dat zorgt er meteen voor dat de totale stroom uit B gelijk is aan de totale stroom in P, immers als voor elk T-knooppunt apart geldt
"in = uit", dan geldt dat ook voor de som van alle T-knooppunten samen.

De totale stroom uit-B en in-P (die zijn dus gelijk) noemen we wel de stroomwaarde van het netwerk (in dit voorbeeld is de stroomwaarde 13). Meestal (nou ja, eigenlijk altijd) zullen we op zoek gaan naar de maximale stroomwaarde van een netwerk.

Vaak is het handig om een netwerk om te bouwen tot een ander netwerk met slechts één Bron en één Put. Dat kan heel eenvoudig: leg vóór alle bronnen één nieuw Bronpunt (B₀) en geef dat punt verbindingslijnen met capaciteit ¥ naar alle B-knopen. Leg ook na alle putten een nieuw Putpunt (P₀) en geef alle P-knopen een verbindingslijn met capaciteit naar dat nieuwe punt. Dat zou er in ons voorbeeld zó uitzien:

Snedes.

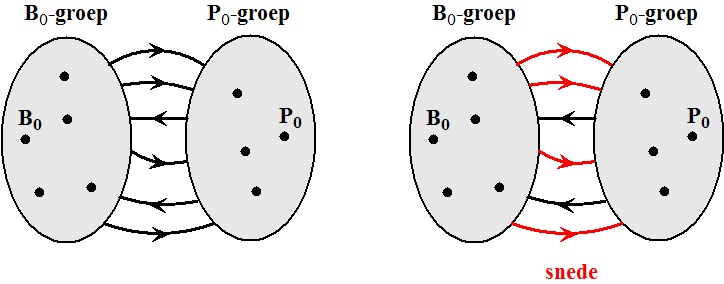
Je maakt als volgt een snede in een netwerk:
Verdeel de knooppunten in twee groepen: eentje (de B₀-groep) met B₀ erin en eentje (de P₀-groep) met P₀ erin.
Een snede bestaat nu uit alle verbindingslijnen die van de B₀-groep naar de P₀-groep lopen.

Hier zie je een B₀-groep (blauw) en een P₀-groep (paars). De rode verbindingslijnen samen vormen een snede. De capaciteit van deze snede is de som van de stromen van de verbindingslijnen. De hier gemaakte snede heeft capaciteit 20. Bedenk goed dat je alleen lijnen VAN de B₀-groep NAAR de P₀-groep moet nemen. Als de verbindingslijn tussen T₃ en T₄ in het bovenstaande voorbeeld de andere kant op had gelopen, dan hoorde hij niet bij de snede!

Stelling.

De stroomwaarde van een netwerk is kleiner of gelijk aan de capaciteit van een snede.

Bewijs:

1. Stromen van B₀-groep naar P₀-groep ≤ Capaciteit snede (meer kan er nou eenmaal niet door).
2. Stroomwaarde ≤ Stromen van B₀-groep naar P₀-groep

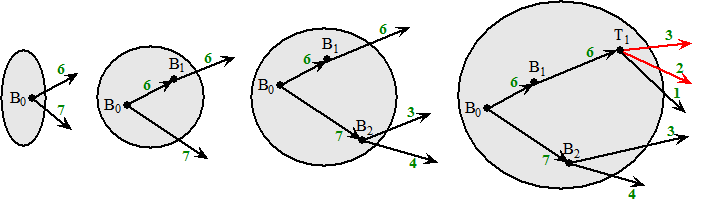
Kijk maar naar dit stripverhaal.
We beginnen met B₀ en gaan de verzameling B₀-knooppunten langzaam uitbreiden. B₀ heeft som van uitgaande stromen 13 en dat is precies gelijk aan de stroomwaarde.
Voeg B₁ toe, en vervang de ingaande stromen naar B₁ door de uitgaande. Dan blijft de som van de uitgaande stromen uit onze verzameling gelijk aan de stroomwaarde. Nog steeds verlaten 6 en 7 onze grijze verzameling.
Voeg op dezelfde manier B₂ toe en vervang de ingaande 7 door de uitgaande 3 en 4. Blijft 13.....
Voeg dan T₁ toe.
Ga net zolang door tot je alle B₀-groep knopen hebt gehad.
Dan is de som van de rode uitgaande pijlen hoogstens gelijk aan de stroomwaarde. Het zou immers kunnen dat er pijlen van de P₀-groep naar de B₀-groep gaan, en die tellen niet mee voor de snede. Dat zou zo bijvoorbeeld zo zijn als je T₁ ook paars zou maken (dus bij de P₀-groep zou zetten). Kijk maar naar deze snede:

Nu zijn de uitgaande stromen uit onze grijze verzameling ineens 14 geworden omdat die verbinding van T₁ naar T₂ niet meetelt. Je ziet dat de snede nu ook 14 is.

uit 1. en 2. volgt direct de stelling.

■

Waarschijnlijk is het intuïtief nog beter te begrijpen wat er aan de hand is als je bedenkt dat de verzamelingen B₀-knopen en P₀-knopen met elkaar verbonden zijn door een aantal (minstens één) verbindingslijnen. Zie de figuur linksonder.

Een snede bestaat uit alle verbindingen van links naar rechts tussen beide verzamelingen. Omdat alle stroom uiteindelijk van B₀ naar P₀ moet, moet dus alle stroom deze snede passeren. Dus kan de totale stroom nooit groter zijn dan de capaciteit van de snede. De snede met minimale capaciteit is zoiets als de "smalste doorsnede" van het netwerk.

Belangrijk gevolg:

maximale stroomwaarde ≤ minimale capaciteit snede

Vanwege de stelling hierboven geeft de snede met de kleinste capaciteit een bovengrens voor de stroomwaarde.

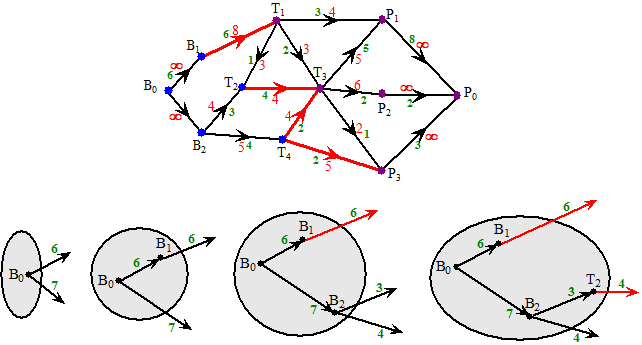
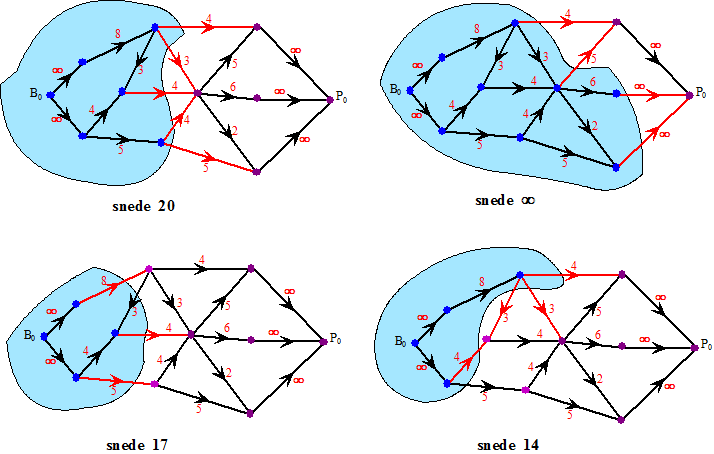
Hier zie je, om er een beetje aan te wennen, een aantal snedes van bovenstaand netwerk. De B₀-groep is steeds aangegeven, en de som van de uitgaande rode lijnen bepaalt de grootte van de snede.

Let nog even op die snede van 17: de ingaande lijn met capaciteit 3 telt niet mee!

Nou zou je om de maximale stroomwaarde te bepalen natuurlijk alle mogelijke snedes kunnen tekenen en dan degene met de kleinste totale som kunnen nemen. Maar dat is nogal een werk: je moet van een verzameling van n knooppunten (B₀ en P₀ niet meegerekend) een willekeurige deelverzameling kiezen. Dat kan op 2ⁿ manieren!!!!

In de volgende les zullen we een snellere manier bekijken om de maximale stroomwaarde te vinden. Je bent vast al nieuwsgierig.....☺