max-flow min-cut

© h.hofstede (h.hofstede@hogeland.nl)

Max-Flow, Min-Cut

De vorige les eindigden we met de stelling "maximale stroomwaarde ≤ minimale capaciteit snede".

Deze les zullen we zien dat het gelijkteken geldt, en tegelijkertijd zullen we een manier vinden om een optimale stroom door een netwerk te vinden.

Eerst (uiteraard) de gebruikelijke termen.
Een stroom in een netwerk is een functie die aan elke verbindingslijn een waarde toekent (zie vorige les; er zijn twee voorwaarden). Zo'n stroom geven we vanaf nu aan met de functie f (van flow) en verbindingslijnen met een v
Dus: stroom = f(v)
Een verbindingslijn heet f-verzadigd als f(v) = c(v), waarbij c de capaciteit van lijn v is. Als f(v) < c(v) dan noemen we de lijn f-onverzadigd.

Een nieuwe functie: t(v) geeft aan hoeveel de stroom door lijn v nog zou kunnen toenemen. Dus: t(v) = c(v) - f(v)
Voor een f-verzadigde verbindingslijn is t(v) = 0 (er is geen toename meer mogelijk).
Ook aan een hele route R kunnen we een t(R) toekennen: dat is de kleinste t van alle verbindingslijnen waaruit R bestaat. (eigenlijk staat daar zoiets als: "Een route kan zoveel toenemen als zijn zwakste schakel"). Een route R heet nu f-onverzadigd als t(R) > 0.
Een route R van B₀ naar P₀ die f-onverzadigd is noemen we een f-vermeerderende route.

Je zult al wel begrijpen dat de stroom in een netwerk nog niet maximaal is zolang er nog zulke f-vermeerderende routes te vinden zijn. Immers daar is nog winst te halen want daar kan de stroom groter.

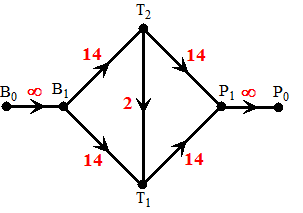
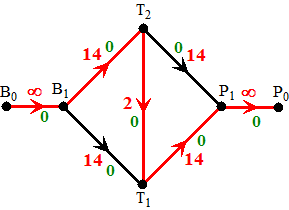
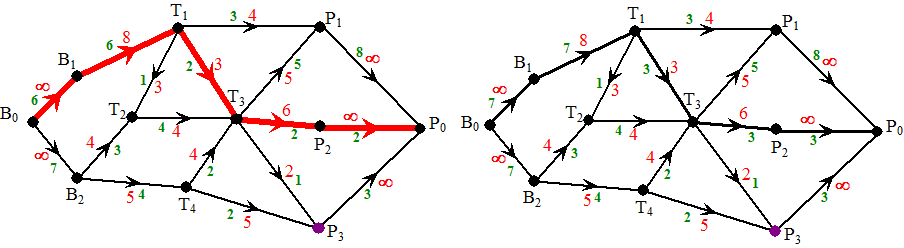
De rode route is een f-vermeerderende route want overal is t(v) > 0. De kleinste t(v) die voorkomt is die van lijn T₁T₃, want daar is t(v) = 1. Daarom kunnen alle stromen met 1 verhoogd worden. Dat geeft de nieuwe stromen rechts met stroomwaarde 14.
Nou; dezelfde procedure dan nog maar een keer:

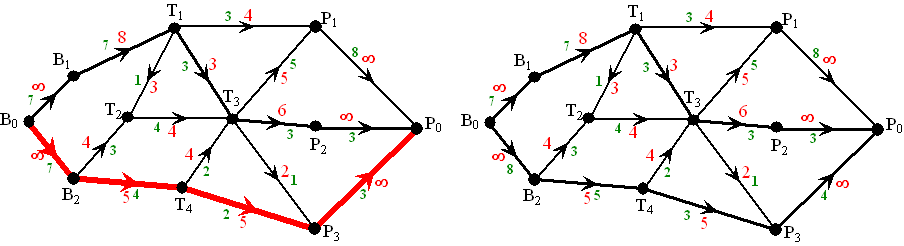
Alweer eentje hoger.
Nou, zo gaan we steeds maar door totdat er geen f-vermeerderende route te vinden is.

Kijk uit met verbindingen de andere kant op!

Daar bedoel ik het volgende mee.
Stel dat je in het netwerk waar we gebleven waren de volgende route kiest:

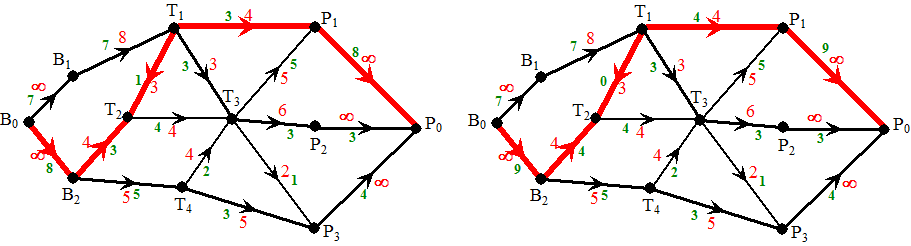
Dan zit daar die rare route T₂T₁ in die "tegen de stroom ingaat". In zo'n geval kun je doen alsof de t(v) gelijk is aan f(v) want door de stroom f(v) nul te maken gaat er meer stroom de andere kant op; dat zie je in de figuur: als je T₂T₁ nul maakt dan kan T₁P₁ eentje hoger worden!
Rechts zie je een verbetering: stroomwaarde is nu al 16.
Voor de netheid moet je dus eigenlijk zeggen:

En de nieuwe stromen in route R met kleinste waarde t(R) worden dan:

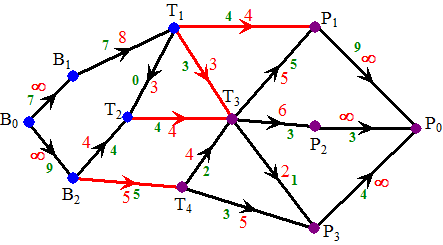
De stroom in bovenstaand netwerk kan nu niet beter. Dat kun je hiernaast zien: in de getekende snede (van blauwe B₀-knopen naar paarse P₀-knopen) hebben alle verbindingen t = 0. Omdat elke route een lijn van deze snede moet passeren heeft elke route t(R) = 0

Je ziet dat de maximale stroomwaarde gelijk is aan de som van de stromen door deze snede (4 + 3 + 4 + 5 = 16)

Een algoritme
(naar Ford & Fulkerson, 1957)

Tot nu toe was het nog "een beetje proberen" om zulke f-vermeerderende routes te vinden. Maar ook daar bestaat gelukkig een algoritme voor.
Wat we gaan doen is het volgende: We beginnen bij B₀ en gaan vanaf daar een boom maken. Maar dat doen we door alleen maar f-onverzadigde verbindingslijnen te gebruiken. Zo'n boom heet dan ook een f-onverzadigde boom.
Dat langzaamaan maken/uitbreiden van de f-onverzadigde boom kan op twee manieren gebeuren ("met de stroom mee"" en ""tegen de stroom in"):

Voeg een f-onverzadigde verbinding toe die loopt van een (knooppunt-van-de-huidige-boom) naar een (knooppunt-nog-niet-van-de-boom).

Voeg een verbindingslijn toe die van een (knooppunt-niet-van-de-huidige-boom) naar een (knooppunt-van-de-boom) loopt en die positieve
f-waarde heeft (dus niet nul).

En nou gaat het er maar om of die boom punt P₀ gaat bereiken. Als dat zo is, dan hebben we een nieuwe f-vermeerderende route gevonden. Na verbeteren van de stroomfunctie beginnen we gewoon weer opnieuw.
Als we P₀ niet kunnen bereiken met onze boom, dan was onze f optimaal.

Blijft nog over de vraag: "Als je meerdere verbindingslijnen aan de boom zou kunnen toevoegen, welke moet je dan nemen?"
Die vraag beantwoorden we door de knooppunten van de boom te nummeren.
Begin met knooppunt B₀ nummer 1 te geven, en elk nieuw aan de boom toegevoegde knooppunt krijgt een volgend nummer.

Het uitbreiden van de boom gaat nu volgens de regel:

Je mag een knooppunt van de boom pas onderzoeken op mogelijke uitbreidingen,
als je alle eerder genummerde knooppunten al hebt geprobeerd.

Deze kleine uitbreiding komt van Edmonds en Karp (1970)

Hier is een heel eenvoudig voorbeeld van wat er anders mis kan gaan:

Neem het super-simpele netwerkje hiernaast.
Je ziet natuurlijk meteen dat de maximale stroomwaarden gelijk is aan 28, maar laten we ons algoritme van het maken van een boom eens gebruiken. Dat doen we eerst zonder die extra voorwaarde.

Begin met overal stroom 0, en ga een boom maken:

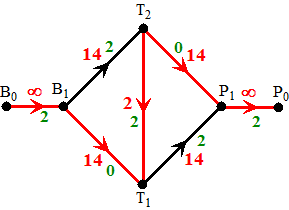
Eerste boom (de keuzes zijn "willekeurig")
Begin bij B₀.
Kies dan B₀B₁ als eerst tak (t = ∞).
Kies dan B₁T₂ als tweede tak (t = 14)
Kies dan T₂T₁ als derde tak (t = 2)
Kies dan T₁P₁ als vierde tak (t = 14)
Dat geeft een f-vermeerderende route met t waarde 2 (de laagste t van de gevonden takken) , dus kunnen we alle stromen in die route 2 verhogen en opnieuw beginnen.

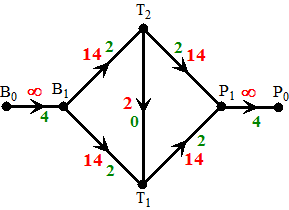
Tweede boom (de keuzes zijn "willekeurig"):
Begin bij B₀.
Kies dan B₀B₁ als eerst tak (t = ∞).
Kies dan B₁T₁ als tweede tak (t = 14)
Kies dan T₂T₁ als derde tak (t = 2, want f = 2 en deze is andersom)
Kies dan T₁P₁ als vierde tak (t = 14)
Dat geeft een f-vermeerderende route met t waarde 2, dus kunnen we alle stromen in die route 2 verhogen (en T₂T₁ nul maken) en opnieuw beginnen.

Zie je al wat er gebeurt?

Het zou kunnen dat we om-en-om de routes B₀B₁T₂T₁P₁P₀ en B₀B₁T₁T₂P₁P₀ kiezen, en elke keer de stroomwaarde met 2 verhogen. Natuurlijk is dat niet een handige keuze, maar zonder voorwaarden aan de manier waarop we de boom uitbreiden zou dit kunnen gebeuren (vooral bij erg grote netwerken waar alles lang niet zo overzichtelijk is als hier).

Maar met onze handige extra voorwaarde kan dat niet meer. Kijk maar:

Handige boom (kies laagste knoopnummer):
Kies B₀ (knoop nr. 1)
Kies B₀B₁ als eerste tak (t = ∞, B₁ = knoop nr. 2)

Kies B₁T₂ als tweede tak (t = 14, T₂ = knoop nr. 3): je mag alleen vanaf B₁ uitbreiden omdat B₀ niet verder wil!!!
Nu mag je niet T₂T₁ kiezen want die loopt vanaf T₂, en T₂ (nr. 3) is later genummerd dan B₁(nr. 2), dus je moet eerst proberen of je vanaf B₁ nog kunt uitbreiden.
Dat geeft automatisch keuze B₁T₁ als derde tak (t = 14, T₁ = knoop nr. 4)
B₁ wil nu niet verder, dus nu moet je eerst vanaf T₂ proberen! (laagste voorradige nummer)
Dat geeft T₂P₁ als tak 4 en daarna de f-vermeerderende route B₀B₁T₂P₁P₀ met t = 14.

Bij de tweede boom vind je dan de route onderlangs voor nog eens t = 14, en dan heb je de maximale stroomwaarde 28 gevonden.

Uitgebreid slotvoorbeeld.

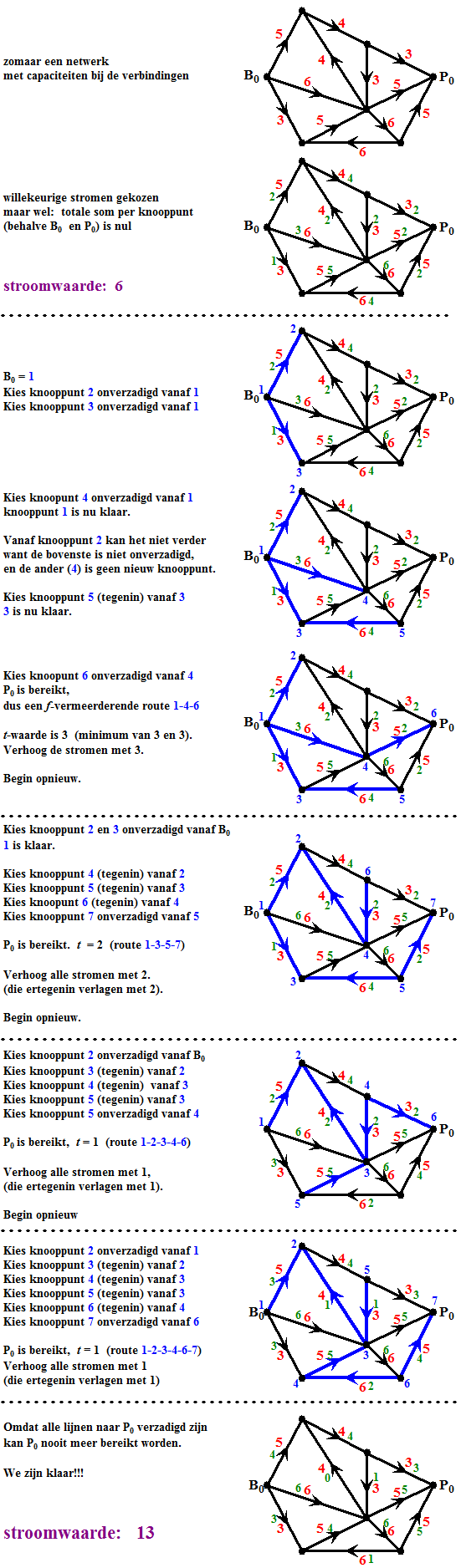
Bedenk in het volgende voorbeeld goed:

BLAUW = knooppuntnummer,
ROOD = capaciteit,
GROEN = huidige stroom.