Poolse notatie

© h.hofstede (h.hofstede@hogeland.nl)

De Poolse notatie.

Dit is een haakjesvrije notatie die werd bedacht door de Poolse logicus Jan Łukasiewicz (op de foto kun je zien wat een knappe man dat was).

Hij verving eenvoudig de derde constructiestap (deze les), door:

als α en β formules zijn, dan zijn ook.
Ùαβ, Úαβ, ⇒αβ, ⇔αβ formules.

Weer valt te bewijzen dat elke geldige formule een unieke constructieboom heeft.

Om een gewone notatie om te zetten in een Poolse volg je gewoon de constructiestappen van de constructieboom.

Om een Poolse notatie weer om te zetten in een "gewone", doe je het volgende:

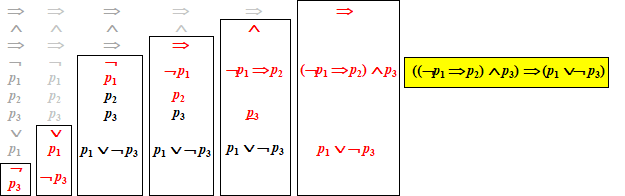
Je leest de formule van rechts naar links, en alle dingen die je tegenkomt leg je op een stapel (volgende steeds bovenop de vorige).
Zodra je met de bovenste "dingen" van je stapel een formule kunt maken doe je dat en vervang je die "dingen" door die hele formule. Dan ga je weer verder met stapelen.

voorbeeld:

⇒ Ù ⇒ ¬ p₁ p₂ p₃ Ú p₁ ¬ p_{3 geeft:}

Het rode wordt steeds uitgevoerd en verschijnt in de volgende kolom. Het eindresultaat is de "gewone" gele formule rechts.

Controlemethode.

Łukasiewicz gaf ook een handige manier om te berekenen of een rij symbolen een geldige formule is.
Die werkte als volgt:

Ken aan de symbolen de volgende getalswaarden toe:

   p_i = -1
    ¬ = 0
    Ù , Ú , ⇒ , ⇔ = 1

Begin nu van links naar rechts in je rijtje symbolen de getalswaarden op te tellen. Als onderweg steeds tussensommen ≥ 0 optreden, en bij het laatste symbool eindig je met -1, dan heb je met een geldige formule te maken (en omgekeerd).

Voorbeeld:

((¬ p₂ ⇒ ¬ p₁) ⇒ (p₁ ⇒ p₂))    wordt in Poolse notatie:

⇒ ⇒ ¬ p₂ ¬ p₁ ⇒ p₁p₂en tellen levert de volgende tussensommen op:1   2   2   1   1   0    1   0 -1

Overal   ≥ 0 en eindigend op -1. Conclusie: dit is een geldige formule.


OPGAVEN

1.	Schrijf in Poolse notatie:

	a.	((p₁ ⇒ (p₂ ⇒ p₃)) ⇒ ((p₁ ⇒ p₂) ⇒ (p₁ ⇒ p₃)))

	b.	((p₁ Ù (p₂ Ú p₃)) ⇔ ((p₁ Ù p₂) Ú (p₁ Ù p₃)))

2.	Ga na of de volgende Poolse-notatie-formules geldige formules zijn, en als dat zo is geef dan hun gangbare notatie.

	a.	⇒ ⇒ ⇒ p₁ ¬ p₂ ¬ p₂ p₁

	b.	¬ p₁ ⇒ p₂

	c.	¬ ⇒ p₁ p₂