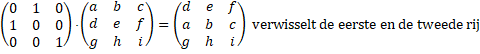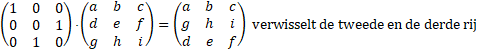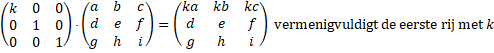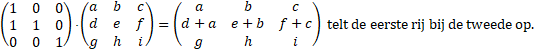elementaire matrices

© h.hofstede (h.hofstede@hogeland.nl)

Elementaire Matrices.

We hebben in de vorige twee lessen steeds gebruik gemaakt van de volgende drie bewerkingen die we met de rijen van een matrix mochten doen:

Twee rijen met elkaar verwisselen.

Een rij met een constant getal vermenigvuldigen.

Een rij een aantal keer bij een andere rij optellen.

Deze bewerkingen kun je ook met behulp van een matrixvermenigvuldiging uitvoeren, en de matrices die daarvoor nodig zijn, heten elementaire matrices. We zullen deze les gaan bekijken hoe ze eruit zien. Later zullen we ze ook nog gaan gebruiken om eigenschappen van matrices af te leiden of te bewijzen.

Ik doe het voor met 3 × 3 matrices.

1. Twee rijen met elkaar verwisselen.

Nou ja, meer is niet nodig: als je de eerste en de derde rij wilt verwisselen, dan wissel je gewoon eerst de eerste en de tweede en daarna de tweede en de derde en dan wer de eerste en de tweede. Ga maar na!

2. Een rij met een constant getal vermenigvuldigen.

Nou ja, meer is niet nodig; als je andere rijen met een constant getal wilt vermenigvuldigen, dan wissel ze je eerst van plaats met de eerste rij, en wissel je ze na het vermenigvuldigen gewoon weer terug.

3. Een rij bij een andere rij optellen.

Nou ja, meer is niet nodig; als je andere rijen bij elkaar op wilt tellen kun je ze eerste met elkaar verwisselen zodat ze op de eerste en tweede rij staan.
En door te combineren met de bewerkingen bij 2) kun je nu ook twee willekeurige rijen een aantal keer bij elkaar optellen.

Je ziet dat je alle rijbewerkingen tot stand kunt brengen door te links vermenigvuldigen met een geschikt gekozen elementaire matrix Ɛ.
Zo'n elementaire matrix is altijd een vierkante matrix. Immers als voor de afmetingen moet gelden dat
(... × ....)(a × b) = (a × b) dan moet op die stipjes wel (a × a) staan. Vierkant dus.

Een matrix maken met Elementaire matrices.

Als je een matrix M hebt waarvan de inverse bestaat, dan kon je die gaan schoonvegen (tot de rref-vorm), en we hebben net gezien dat dat kan door met elementaire matrices te vermenigvuldigen.
Dus er zijn Ɛ's te vinden zodat: Ɛ₁Ɛ₂Ɛ₃....Ɛ_kM = I
Maar omdat elke elementaire matrix een inverse heeft, kun je al die vermenigvuldigingen stuk voor stuk wegwerken door de links te vermenigvuldigen met Ɛ^-1:
Ɛ₁^-1 Ɛ₁Ɛ₂Ɛ₃....Ɛ_kM = Ɛ₁^-1E
Ɛ₂Ɛ₃....Ɛ_kM = Ɛ₁^-1E
Ɛ₂^-1 Ɛ₂Ɛ₃....Ɛ_kM = Ɛ₂^-1 Ɛ₁^-1 E
Ɛ₃....Ɛ_kM = Ɛ₂^-1 Ɛ₁^-1E

Dat geeft uiteindelijk: M = Ɛ_n^-1 ....Ɛ₂^-1Ɛ₁^-1
Maar nou komt het: Alle elementaire matrices hebben een inverse! Ga dat zelf maar na door bij de drie voorbeelden hierboven de determinanten uit te rekenen: er is er geen eentje gelijk aan nul.

Dus staat hier M geschreven als een product van elementaire matrices.

Elke inverteerbare matrix M is te schrijven als product van Elementaire matrices

De determinant van Ɛ • A

Er waren drie mogelijke varianten van Ɛ

Twee rijen verwisselen.
Dan is |Ɛ| ontstaan door van de eenheidsmatrix twee rijen te verwisselen, dus = |Ɛ| = -1.
Maar dan is | Ɛ • A| = -|A| = | Ɛ | • |A|

Een rij met een constant getal vermenigvuldigen
Dan is |Ɛ| ontstaan door van de eenheidsmatrix een rij met k te vermenigvuldigen dus = |Ɛ| = k.
Maar dan is | Ɛ • A | = k • |A| = |Ɛ| • |A|

Een rij bij een andere rij optellen
Dan is |Ɛ| ontstaan door van de eenheidsmatrix een rij bij een andere op te tellen, dus |Ɛ| = 1.
Maar dan is | Ɛ • A | = 1 • |A| = |Ɛ| • |A|

Er is maar één conclusie mogelijk:

| Ɛ • A | = | Ɛ | • |A|

De determinant van A • B

We bekijken twee gevallen.

Geval 1. A is niet inverteerbaar; |A| = 0
Als A niet inverteerbaar is, dan is A • B ook niet inverteerbaar.
Dus is | A • B | = 0
Het doet er niet toe hoe groot | B | is, er geldt altijd | A • B | = | A | • | B |

Geval 2. A is wel inverteerbaar
Dan kun je A dus schrijven als product van elementaire matrices (stelling bovenaan).
A = Ɛ₁• Ɛ₂ • Ɛ₃ ....
A • B =(Ɛ₁• Ɛ₂ • Ɛ₃ ....) • B
|A • B| = |Ɛ₁ • Ɛ₂ • Ɛ₃ .... • B | = |Ɛ₁| • |Ɛ₂| • |Ɛ₃|...• |B|

maar ook:
|A| = | A • E | = |Ɛ₁ • Ɛ₂ • Ɛ₃ ...• E| = |Ɛ₁| • |Ɛ₂| • |Ɛ₃|...1 = |Ɛ₁| • |Ɛ₂| • |Ɛ₃|... (E is immers de eenheidsmatrix)

Als je beiden met elkaar vergelijkt dan zie je dat moet gelden:

| A • B | = |A| • |B|