stelling van Vizing

© h.hofstede (h.hofstede@hogeland.nl)

De stelling van Vizing.

In de vorige les ontdekten we dat in het algemeen geldt voor lijnkleuringen dat χ' ≥ Δ en dat in het speciale geval van een bipartiete graaf geldt χ' = Δ .
In 1964 bewees Vadim Vizing een preciezere bewering, namelijk de volgende:

Voor elke enkelvoudige graaf geldt: χ' = Δ of χ' = Δ + 1

Daarmee vallen de grafen dus in twee klassen uiteen: de grafen met χ' = Δ (waar zoals we al zagen de bipartiete grafen bijhoren) en de grafen met χ' = Δ + 1.

Het bewijs dan maar?

We gaan het bewijs leveren met behulp van volledige inductie.
Stel dat elke graaf met n verbindingslijnen inderdaad (Δ + 1) - lijnkleurbaar is (onze inductie-aanname).

Neem vervolgens een graaf met n + 1 verbindingslijnen.

Bekijk daarvan een knooppunt K₀ .

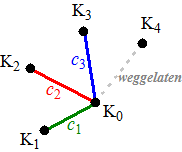
Laten we de buren van K₀ gaan nummeren: K₁, K₂, K₃, K₄, ... met verbindingskleuren c₁, c₂, c₃, c₄, ... Stel dat we dat hebben gedaan tot en met een bepaalde K_m met kleur c_m (in de figuur hiernaast m = 4). Dan is de graad van K0 dus minstens m.

Laat nu K₀K_m weg.
Dan is de resterende graaf dus (Δ + 1) - lijnkleurbaar, want die heeft een verbindingslijn minder (inductieaanname). De graad van de resterende graaf is minstens m - 1 dus er zijn m kleuren beschikbaar.

Stel dat kleur c₀ NIET aan K₀ voorkomt (zo'n kleur is er zeker, want de graad van K₀ is kleiner dan Δ en er zijn Δ + 1 kleuren voorradig). Neem bijvoorbeeld c₀ = paars in het voorbeeld hiernaast (die zit zoals je ziet niet aan K₀). Dan nemen we maar aan dat die c₀ WEL aan K_m zit (anders kleuren we meteen K₀K_m in kleur c₀ en zijn we klaar).

Dus is er, behalve c₀, een "nieuwe" kleur c_m die tot nu toe nog NIET aan K₀ voorkomt. Neem in het voorbeeld c₄ = bruin.

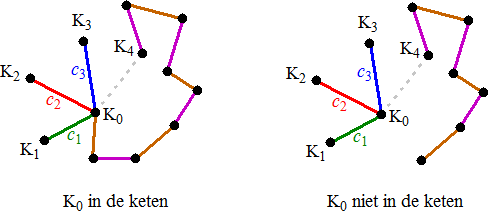
We gaan nu vanaf knooppunt K_m een zogenaamde Kempe-keten maken, met de kleuren c₀ en c_m
Dat gaat zo: neem de verbindingslijn met kleur c₀ vanaf K_m naar een buurpunt

Ga vanaf dat nieuwe buurpunt via c_m naar een volgend buurpunt, dan weer via c₀ verder en zo steeds om-en-om totdat het niet verder wil.

Dat geeft in ons voorbeeld een paars-bruine Kempe-keten.

Nu zijn er twee mogelijkheden voor deze Kempe-keten:

K₀ zit NIET aan de keten.
in dat geval kun je in de keten alle kleuren c₀ en c_m_{+ 1} wisselen. Dan is daarna K₀K₄ met kleur c₀ te kleuren want die zit aan beiden niet (in ons voorbeeld rechts zou je K₀K₄ paars kunnen maken en alle andere paars-bruine omwisselen).
In dat geval is de graaf met de extra verbindingslijn K₀K₄ dus ook kleurbaar!

K₀ zit WEL aan de keten. Dan moet de keten daar via kleur c_m eindigen (doorgaan via c₀ kan nu niet want c₀ zat immers niet aan K₀).
Maar dan is er dus kennelijk een nieuw buurpunt K_{m + 1} van K₀ te vinden met kleur c_m , immers c_m kwam nog niet voor bij de andere buurpunten K₁, ...K_m-1 en K_m zelf was niet meer verbonden met K₀).

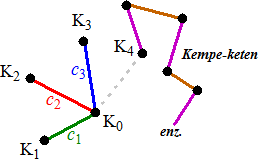
In geval 1 hebben we meteen aangetoond dat G kleurbaar is.
In geval 2 gaan we het hele verhaal gewoon wéér toepassen, nu met de buurpunten K₁, K₂, ..., K_{m + 1}
Dus laat K₀K_{m + 1} weg, en nummer de rest K₁, ..., K_m met kleuren c₁, ...c_m

Herhaal het hele proces hierboven.

Als dat weer een "geval 1" oplevert zijn we weer klaar.
Als dat wéér een "geval 2" oplevert gaan we het nog een keer doen, nu met genummerde buren K₁, K₂, ..., K_{m
+ 2}
Maar omdat de graad van K₀ eindig is, kunnen we niet eeuwig geval 2 krijgen.
Er moet een keertje geval 1 komen......
Dus is G (Δ + 1) - lijnkleurbaar.

q.e.d.

Het mooie van dit bewijs is dat het meteen ook een methode levert om zo'n kleuring te maken!