gerichte grafen

© h.hofstede (h.hofstede@hogeland.nl)

Gerichte grafen.

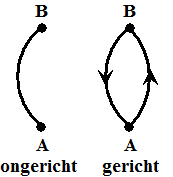
Een gerichte graaf is een graaf waarin verbindingslijnen een richting hebben. Het zijn geen gewone lijnen, maar pijlen met een beginknooppunt en een eindknooppunt.

Laten we dan voor het gemak maar zeggen dat ALLE verbindingslijnen een richting hebben. Alle lijnen zonder richting kun je eenvoudig zoals hiernaast veranderen in twee lijnen met een richting.
Het enige is, dat we het dan vanaf nu niet meer hebben over enkelvoudige grafen.....

Oké: tijd voor het gebruikelijke zootje nieuwe termen:
Zo'n gerichte graaf noemen we vanaf nu een digraaf (van directed graph), en geven we aan met de letter D (ipv G)

De graaf G die je krijgt door alle verbindingslijnen van een digraaf "gewoon" te maken (dus door simpel alle pijlen weg te laten) heet de onderliggende graaf G van de digraaf. En omgekeerd heet de digraaf D dan een oriëntatie van G. De routes in een digraaf zijn uiteraard gerichte routes, en twee knooppunten heten verbonden als elk vanuit de ander te bereiken is via zo'n gerichte route (let op: beide kanten op dus!!). Een graaf heet verbonden als alle knooppunten verbonden zijn (dus als elke op één of andere manier vanuit elke andere te bereiken is).
Elk knooppunt van een digraaf heeft nu een ingraad (= aantal inkomende verbindingslijnen) en een uitgraad (= aantal vertrekkende verbindingslijnen).

Steling 1.

Elke digraaf heeft een (gerichte) route van lengte χ - 1 (verbindingslijnen)

Bewijs.

Laat uit de graaf zo weinig mogelijk verbindingslijnen weg, zodat er nét geen cykel meer is. De nieuwe graaf die je dan krijgt noemen we D' (dat is dus de grootst mogelijke deelgraaf van D die geen cykels meer heeft).
Stel nu dat de langste route in D' lengte L heeft.
We gaan nu alle knooppunten van D' op een speciale manier kleuren. Dat doen we door eerst alle kleuren een nummer 1, 2, 3, 4... te geven en daarna een knooppunt te kleuren volgens het recept: "Geef een knooppunt kleur n als de langste route vanaf dat knooppunt gelijk is aan n + 1"
Bijvoorbeeld zó:

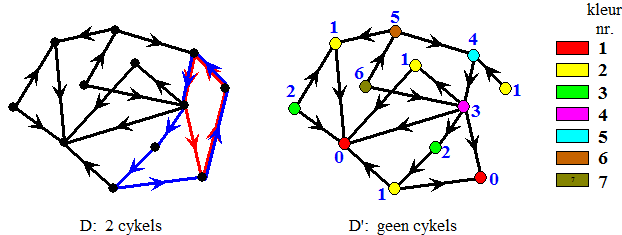
Links zie je een graaf met twee cykels (een rode en een blauwe). Daarnaast is zo'n rood-blauwe lijn weggelaten zodat beide cykels zijn verdwenen.
Het kleurvoorschrift helemaal rechts kleurt de graaf D' zoals je ernaast ziet (het blauwe nummer bij de knopen geeft de grootst mogelijke route vanaf zo'n knoop).
Deze manier van kleuren blijkt een geldige kleuring voor de hele graaf D te zijn!!

Waarom is dat zo?
Kijk, dat dat voor D' geldt lijkt me logisch: twee knooppunten in D' naast elkaar kunnen nooit dezelfde kleur hebben want de langste route vanaf één van beiden is altijd eentje groter dan vanaf andere (er komt immers één stap bij, namelijk de verbindingslijnen van beide knooppunten zelf). Sterker nog: op elke route hebben alle knooppunten verschillende kleur!!!

Maar waarom blijft de kleuring geldig als we de weggelaten lijnen uit D weer toevoegen? Je ziet dat dat in het voorbeeld inderdaad zo is: de weggelaten lijn daar helemaal rechts is rood-geel dus kan weer toegevoegd worden. Maar waarom is dat altijd zo?????

Dat kun je als volgt zien: Als je een weggelaten lijn weer toevoegt, dan ontstaat er een cykel C (immers D' was de grootste graaf zonder cykel). Maar dan is die cykel zonder die toegevoegde verbinding óók een route uit D', dus hebben die twee knopen altijd verschillende kleur (in het voorbeeld hierboven móest er wel een route in D' van dat gele naar dat rode punt lopen, anders was er geen cykel in D).

Er bestaat dus een goede kleuring van D met n + 1 kleuren dus moet χ wel kleiner of gelijk aan n + 1 zijn
En als χ ≤ n + 1 dan is n ≥ χ - 1

■

Je kunt deze stelling natuurlijk andersom gebruiken om van een graaf met chromatisch getal χ een oriëntatie te maken met als langste route χ - 1. Geef alle kleuren gewoon een nummer en richt alle pijlen steeds van een hoger naar een lager nummer!!!

Toernooien

Een toernooi is de oriëntatie van een volledige graaf. Dus in een toernooi loopt er van ieder knooppunt naar iedere ander knooppunt precies één gerichte verbindingslijn. De naam "toernooi" is logisch want een "echt" toernooi waarin ieder precies één keer tegen ieder ander speelt (een halve competitie) geeft namelijk zo'n graaf: je kunt een verbindingslijn dan lezen als "heeft gewonnen van ".

Stelling 2.

Elk toernooi heeft een (gerichte) Hamiltonroute

(een Hamiltonroute is een route met elk knooppunt precies één keer erin, weet je nog?)

Bewijs:
Het bewijs kan in één regel:
"In een toernooi is χ gelijk aan het aantal knooppunten K, dus er is een route van lengte K - 1 verbindingslijnen (stelling 1), dus die moet wel K knooppunten verbinden".

■

Voor de volgende stelling hebben we weer wat termen nodig:
Een inbuur van een knooppunt K is een knooppunt vanwaar een verbindingslijn naar K loopt.
Een uitbuur van een knooppunt K is een knooppunt waar een verbindingslijn vanaf K naar toeloopt.
Een onafhankelijke verzameling knooppunten uit een graaf is een verzameling knooppunten waarvan geen enkel tweetal direct verbonden is.

Stelling 3.

Een digraaf zonder cykels heeft altijd een onafhankelijke verzameling knooppunten
van waaruit elk knooppunt in hoogstens twee stappen te bereiken is.

Bewijs.

Met inductie.
Het geldt uiteraard voor een graaf met 1 knooppunt.
Stel dat de stelling geldt voor elke graaf met minder dan n knooppunten.
Bekijk dan een knooppunt K van een graaf met n knooppunten.
In de graaf zonder K is (inductie-aanname) dus een onafhankelijke verzameling S te vinden van waaruit elk knooppunt in hoogstens twee stappen te bereiken is.
Voor K zijn er nu twee mogelijkheden:

K is een uitbuur van een knooppunt van S dan is K ook bereikbaar vanaf S

K is van geen enkel punt van S een uitbuur. Dan is K niet verbonden met S dus is de verzameling S ∪ K een nieuwe onafhankelijke verzameling waar de eigenschap voor geldt.

In beide gevallen geldt de eigenschap dan ook voor de graaf met n knooppunten.

■

Gevolg: Elk toernooi heeft een knooppunt van waaruit elk ander knooppunt in hoogstens twee stappen te bereiken is.
Immers in elk toernooi zijn alle knooppunten verbonden dus bestaat de maximale onafhankelijke verzameling uit één knooppunt!

Stelling 4.

als D een verbonden toernooi is met n knooppunten (n ≥ 3),
dan is elk knooppunt van D deel van een 3-cykel, een 4-cykel, .... , een n-cykel

(een verbonden toernooi was een toernooi waarin elk knooppunt op de één of andere manier vanuit elk ander knooppunt te bereiken is, wist je nog?).

Bewijs.

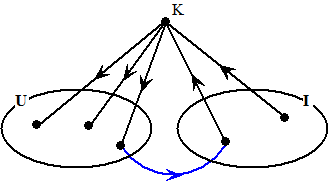
Kies een willekeurig knooppunt K van D. Noem de verzameling van alle uitburen van K de verzameling U en de verzameling van alle inburen de verzameling I.

We bewijzen eerst dat K in een 3-cykel zit:
Omdat D verbonden is kunnen B en I niet leeg zijn, en moet er ook minstens één verbindingslijn van U naar I zijn. Als zo'n blauwe lijn als hiernaast er niet zou zijn kun je I niet bereiken vanaf de U-knooppunten, immers U, I en K zijn samen alle knooppunten van de graaf.
Maar dan is er dus een 3-cykel waar K in zit.

We gaan nu verder met inductie.
Stel dat knooppunt K in een 3, 4, ..., n cykel zit (inductie-aanname), dan zullen we aantonen dat K dan ook in een
n + 1 - cykel zit. Dat gaat als volgt.

Laten we alle knooppunten uit de n-cykel waar K in zit C_n noemen. Nu zijn er twee mogelijkheden:

Mogelijkheid 1. Er is een nieuw knooppunt K₁ te vinden is dat een uitbuur van een knooppunt uit C_n is, en ook een inbuur van een knooppunt van C_n .
Dan kun je een C_{n + 1}-cykel maken, kijk maar:

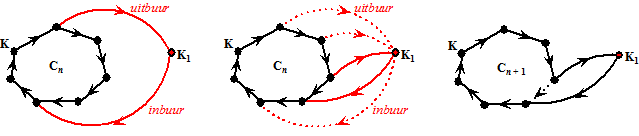
K₁ heeft een inbuur en een uitbuur in C_n. Begin nu bij de uitbuur en volg C_n net zolang tot je twee opeenvolgende knooppunten hebt waarvan de eerste een uitbuur is en de volgende een inbuur (die moeten er zijn anders vind je nooit een inbuur en je weet dat die er is!) In de middelste tekening zijn die gevonden.
Maar dan heb je zoals je rechts ziet ook een n + 1-cykel gevonden!

Mogelijkheid 2. Alle andere knooppunten zijn OF alleen maar uitburen van C_n-knopen OF alleen maar inburen.
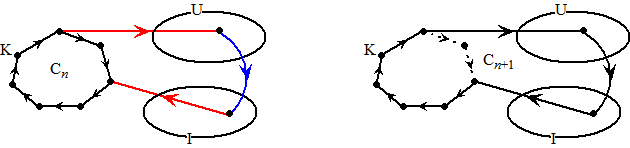
In dat geval maken we (net als hierboven) weer een verzameling I van de inburen van C_n en een verzameling U van de uitburen van C_n. Er moet weer ergens van U naar I een verbindingslijn lopen (anders was D niet verbonden, want dan zijn de I-knopen niet te bereiken).

Neem nu de verbindingslijn van dat blauwe U-knooppunt met een knoop van C_n en de verbindingslijn van het blauwe I-knooppunt twee knopen verderop in C_n (dat kan, immers alle I-knopen lopen naar C_n-knopen toe; het waren immers allemaal inburen!).
En jawel: ook nu heb je een C_{n + 1}-cykel gevonden. Zie de figuur rechts.
Daarmee is het inductiebewijs voltooid.......

■

Overigens volgt uit deze stelling direct dat elk verbonden toernooi een Hamilton-cykel heeft (er is immers een n-cykel!). Wacht, dat is belangrijk genoeg voor een kadertje:

Elk verbonden toernooi heeft een Hamilton-cykel.