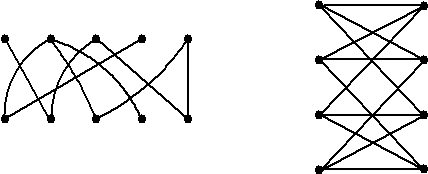|
|||||||||||||
| Verbindingslijnen Kleuren. | |||||||||||||
| Je kunt natuurlijk
ook gaan proberen niet de knooppunten maar de verbindingslijnen van een
graaf te gaan kleuren. In dat geval mogen er bij één knooppunt niet twee
lijnen met dezelfde kleur komen. Dat kun je op twee manieren proberen. 1. Gewoon een beetje gaan proberen. 2. De graaf gaan veranderen in een lijngraaf, en dan daarvan de knooppunten kleuren. |
|||||||||||||
| De lijngraaf van een
graaf maak je door alle verbindingslijnen als knooppunten te nemen, en
die met elkaar te verbinden als ze in de oorspronkelijke graaf bij het
zelfde knooppunt samenkwamen. Voorbeeldje? |
|||||||||||||
|
|
|||||||||||||
| Hier zie je hoe je in
5 stappen van een graaf een lijngraaf maakt. Geef als hulpje eerst de lijnen allemaal een kleur (B) en maak van die kleuren knooppunten (C) Verbind daarna de knooppunten met elkaar als de lijnen in de oorspronkelijke graaf ergens bij elkaar kwamen (D). Laat tot slot de kleuren weer weg (E). |
|||||||||||||
| Een paar simpele stellinkjes over lijnkleuringen. | |||||||||||||
|
|||||||||||||
| Stellinkje 1: | |||||||||||||
|
|||||||||||||
| (Δ was de hoogste graad van alle knooppunten, wist je nog?) | |||||||||||||
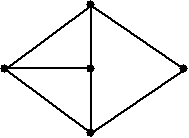
| Bewijs: Lijkt me nogal logisch: voor het knooppunt dat graad Δ heeft zijn al Δ kleuren nodig, immers daar komen Δ verbindingslijnen samen. In de volgende graaf zie je een voorbeeld waarin Δ niet genoeg is: |
|||||||||||||
|
|
|||||||||||||
| De hoogste graad is 3, maar er zijn 4 kleuren nodig om de lijnen te kleuren. Ga dat zelf maar na.... | |||||||||||||
| ■ | |||||||||||||
| Stellinkje 2: | |||||||||||||
|
|||||||||||||
| Bewijs: Stel eerst dat G een Eulergraaf is. • Als alle knooppunten graad 2 hebben dan is G dus een even cykel en volgt de stelling simpel door alle lijnen om-en-om te kleuren. |
|||||||||||||
| • In de andere
gevallen heeft G een knooppunt met graad minstens 4. Noem dat knooppunt
K0. Bekijk dan de Eulerroute K0K1K2....K0 dus de route die begint en eindigt in K0 , en kleur daarvan elke verbindingsweg om-en-om in de eerste kleur en de tweede kleur. Dan komen die twee kleuren inderdaad beide bij alle knooppunten voor, immers elk knooppunt dat je passeert krijgt twee kleuren. |
|||||||||||||
| Stel nu dat G geen
Eulergraaf is. Voeg dan een nieuw knooppunt X toe, en verbind dat met alle knooppunten die oneven graad hebben. De nieuwe graaf is dan wel een Eulergraaf en die kun je als hiervoor kleuren. Ga zelf maar na dat graaf G zonder dat knooppunt X nu ook die eigenschap heeft..... |
|||||||||||||
| ■ | |||||||||||||
|
|
|||||||||||||
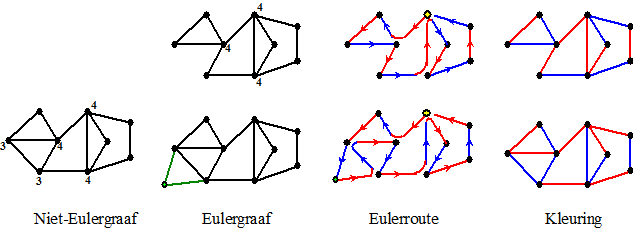
| Hier zie je wat er
aan de hand is. Op de bovenste staat een Eulergraaf en een Eulerroute
daarin geeft meteen een kleuring. In de onderste rij is eerst een extra knooppunt (groen) toegevoegd om de graaf Eulergraaf te maken, vervolgens wordt er een Eulerroute gemaakt, en op het eind wordt dat extra knooppunt gewoon weer weggehaald. |
|||||||||||||
| Bipartiete Grafen | |||||||||||||
| Een
bipartiete graaf is een graaf
waarvan je de knooppunten in twee verzamelingen V en W kunt verdelen
zodat elke verbindingslijn een lijn van V naar W is. Hieronder zie je twee voorbeelden (de rechter is trouwens de verbindingsgraaf van de hoekpunten van een kubus, zie je dat?). Een volledige bipartiete graaf tussen twee verzamelingen van m en n knooppunten wordt aangegeven met Km, n |
|||||||||||||
|
|
|||||||||||||
| Stellinkje 3: | |||||||||||||
|
|||||||||||||
| (Dit is trouwens de "stelling van König" ) | |||||||||||||
| Lemmaatje
vooraf: Stel dat we een optimale kleuring van een bipartiete graaf hebben gemaakt. Stel nu verder dat er een knooppunt K te vinden is waarbij kleur i niet voorkomt en kleur j tweemaal (of vaker) Dan is de graaf met alleen maar de lijnen van kleuren i en j een oneven cykel! Bewijsje: Noem die graaf met alleen de kleuren i en j graaf Gij Stel dat Gij géén oneven cykel is; dan kun je volgens stellinkje 2 hierboven Gij gaan herkleuren met de kleuren i en j zodat bij elk knooppunt wél beide kleuren aanwezig zijn. Dat geeft ook een nieuwe kleuring van de oorspronkelijke graaf G (voeg de andere kleuren weer toe) In die nieuwe kleuring is het aantal kleuren bij knooppunt K dus één groter dan in de oorspronkelijke, immers nu is ook kleur i vertegenwoordigd. Maar dan was de kleuring dus niet optimaal! Dat geeft een tegenspraak, dus is G wél een oneven cykel. |
|||||||||||||
| Terug naar
stellinkje 3: Neem nu een graaf G waarvoor geldt χ' > Δ en stel dat we daar een optimale Δ-kleuring van hebben gemaakt. Dan is er dus nog een knooppunt waar een kleur minstens dubbel voorkomt (immers anders was het chromatisch getal niet groter dan Δ) Maar dan moet er ook wel een andere kleur niet voorkomen bij dat knooppunt (want de hoogste graad is Δ) Dus voldoet de graaf aan de voorwaarden van het lemmaatje hierboven, dus bevat de graaf een oneven cykel. Maar een bipartiete graaf kán geen oneven cykel bevatten!! Als je in V begint ben je na één verbindingslijn in W, na 2 weer in V, na 3 weer in W enzovoorts. Met een oneven aantal verbindingslijnen kun je nooit van V weer in V komen. Kortom: voor een bipartiete graaf kan niet gelden χ' > Δ |
|||||||||||||
| ■ | |||||||||||||
|
Nog een bewijs, maar nu direct met
een kleurrecept erbij. Het recept om een bipartiete graaf met hoogste graad Δ te kleuren gaat zó (meteen maar met een voorbeeld): |
|||||||||||||
| Neem de bipartiete
graaf hieronder. De hoogste graad is 3, dus het moet volgens de stelling met 3 kleuren kunnen... Stel dat we al een poosje aan het proberen zijn te kleuren, en dat we al een aantal lijnen hebben gekleurd met rood, blauw en groen. Daarbij hebben we ervoor gezorgd dat nooit twee dezelfde kleuren bij een knooppunt samenkomen. |
|||||||||||||
|
|
|||||||||||||
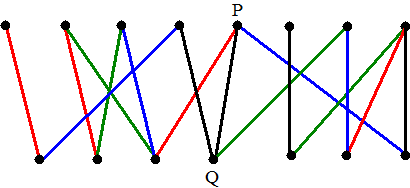
| Kies nu een nog niet
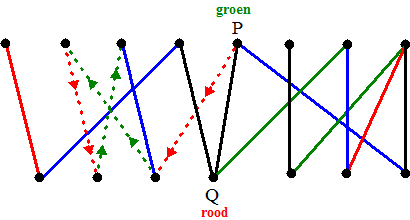
gekleurde lijn, bijvoorbeeld PQ hierboven. Dan is er dus een kleur die nog niet voorkomt bij punt P (kleur cP) en ook een kleur die nog niet voorkomt in punt Q (kleur cQ). Als cP = cQ dan kunnen we direct lijn PQ in die kleur kleuren. Neem daarom aan dat cP en cQ verschillend zijn. Neem in ons voorbeeld cP = groen en cQ = rood Nu gaan we vanaf P een route tekenen met om-en-om de kleuren cQ en cP. Maak die route zo lang mogelijk. Die route kan nooit in Q eindigen, immers naar beneden toe is steeds rood, en omhoog steeds groen. Hieronder staat een zo lang mogelijke route gestippeld getekend: |
|||||||||||||
|
|
|||||||||||||
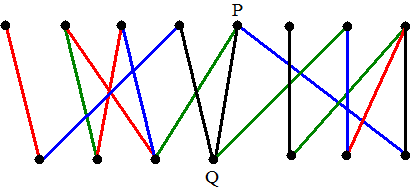
| En nou de grote truc:
je mag de kleuren cP en cQ van die
gestippelde route ook wel met elkaar verwisselen!!! Immers bij alle tussentijds gepasseerde punten komen toch al een rode en een groene lijn samen, dus die mag je best omwisselen. En bij het laatste punt zit geen rode lijn (als dat wel zo was, dan was dit niet de langste route) Wissel daarom de gestippelde rode en groene kleuren: |
|||||||||||||
|
|
|||||||||||||
| Maar kijk: nu
is voor lijn PQ ineens de kleur rood beschikbaar geworden! Kleur PQ rood, en ga op zoek naar de volgende nog niet gekleurde lijn. Daarmee herhaal je gewoon dit recept! En zo alsmaar door totdat alle lijnen zijn gekleurd. |
|||||||||||||
| OPGAVEN | |||||||||||||
| 1. | Toon aan dat voor een
enkelvoudige bipartiete graaf geldt: V ≤ 1/4K2
(V is het aantal verbindingslijnen, K het aantal knooppunten) |
||||||||||||
| 2. | Je kunt de 8
hoekpunten van een kubus "nummeren" met de getallen 0 tm 8
en die dan in het tweetallig stelsel opschrijven. Dat geeft de 8
knooppunten 000, 001, 010, 011, 100, 101, 110, 111. Als je nu twee knopen met elkaar verbindt als ze precies één teken (1 of 0) van elkaar verschillen, dan krijg je de zogenaamde "kubusgraaf". |
||||||||||||
| a. | "Nummer" de hoekpunten van een kubus en laat zien dat je dat zó kunt doen dat de verbindingslijnen van de kubusgraaf precies de ribben van de kubus worden. | ||||||||||||
| b. | Laat zien dat de zo verkregen graaf bipartiet is. | ||||||||||||
| Omdat elk knooppunt van de graaf graad 3 heeft wordt deze graaf wel de 3-kubusgraaf genoemd. | |||||||||||||
| c. | Toon aan dat elke n-kubus graaf bipartiet is. | ||||||||||||
| 3. | a. | Hoeveel verbindingslijnen heeft Km, n ? | |||||||||||
| b. | Voor welke m en m is Km,n regulier? | ||||||||||||
| c. | Voor welke m en m is Km,n een Eulergraaf? | ||||||||||||
| 4. | Toon aan dat de
lijngraaf van een reguliere graaf weer regulier is. Hoe volgt de graad van de lijngraaf uit de graad van G zelf? |
||||||||||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||||||||||