| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
| |
 |
|
ExponentiŽle groei aantonen. |
| |
| Laten we een
willekeurige tabel nemen: |
| |
|
|
|
| t |
4,0 |
7,0 |
9,2 |
12,8 |
| N |
7,43 |
16,31 |
29,06 |
74,72 |
|
| |
|
|
|
De vraag is nu:
beschrijft deze tabel een exponentieel verband, en kunnen we daar een
formule van vinden?
We kunnen nu niet gewoon kijken of de N-getallen elke keer met
dezelfde factor worden vermenigvuldigd, omdat de stapjes van de t niet
even groot zijn.
Laten we het daarom per geval apart bekijken:
|
| ē |
Tussen t = 4,7
en t = 7,0 neemt N toe met groeifactor 16,31/7,43
= 2,1951
Maar dat zijn 3 stapjes, (van 4,0 naar 7,0) dus g3
= 2,1951
De GR geeft dan g = 1,3 (Y1 = X^3 en Y2 =
2,1951 en dan intersect) |
| ē |
Tussen t = 7,0
en t = 9,2 neemt N toe met groeifactor 29,06/16,31
= 1,7817
Maar dat zijn 2,2 stapjes, (van 7,0 naar 9,2) dus g2,2
= 1,7817
De GR geeft dan g = 1,3 (Y1 = X^2,2 en Y2 =
1,7817 en dan intersect) |
| ē |
Tussen t = 9,2
en t = 12,8 neemt N toe met groeifactor 74,72/29,06
= 2,5712
Maar dat zijn 3,6 stapjes, (van 9,2 naar 12,8) dus g3,6
= 2,5712
De GR geeft dan g = 1,3 (Y1 = X^3,6 en Y2 =
2,5712 en dan intersect) |
| |
|
|
|
| Alle gevonden g's
zijn gelijk dus er is sprake van exponentiŽle groei. |
| |
|
|
|
| exponentiŽle groei:
alle g's zijn gelijk. |
|
| |
|
|
|
We weten nu dat de
g per stapje gelijk is aan 1,3.
De formule wordt dan N = B ē 1,3t
Kies nu een willekeurig punt van de tabel, bijvoorbeeld t
= 4,0 en N = 7,43
Vul dat in: 7,43 = B ē 1,34,0
dus 7,43 = B ē 2,8561
Dan is B = 7,43/2,8561 = 2,6
De formule is dus N = 2,6 ē 1,3t |
| |
|
|
|
|
Grafieken van exponentiele groei. |
| |
|
|
|
ExponentiŽle
grafieken zijn altijd gekromde grafieken, maar er zijn twee soorten.
Er zijn grafieken die toenemen (stijgen) en grafieken die afnemen
(dalen).
Dat is natuurlijk ook logisch, want als g groter dan 1 is, dan
neemt de hoeveelheid toe, en als g kleiner dan 1 is, dan is er
afname.
Dat geeft de volgende twee soorten grafieken: |
| |
|
|
|
|
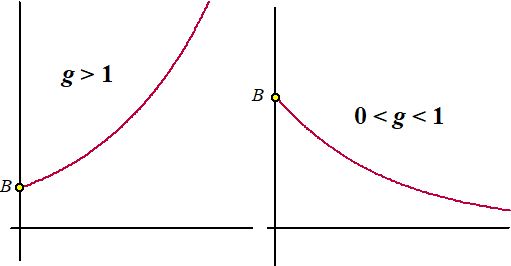 |
| |
|
|
|
Je ziet dat de B
het beginpunt op de y-as is, net zoals bij rechte lijnen dat b
was (van y = ax + b, weet js nog?).
0 < g < 1 betekent dat g tussen 0 en 1 zit (gevallen
waarbij g kleiner dan 0 is zullen we niet tegenkomen).
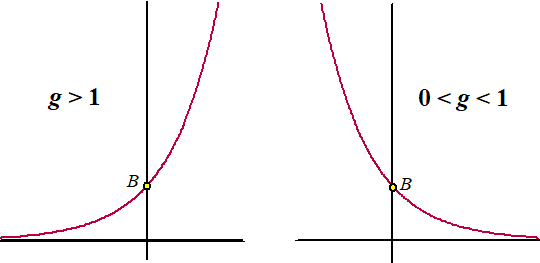
Bovenstaande grafieken zijn alleen getekend voor x > 0 omdat dat
in de meeste gevallen ook zo is.
Als je ze doortrekt voor x < 0 dan krijg je de volgende twee
grafieken: |
| |
|
|
|
|
 |
| |
|
|
|
| |
|
|
|
OPGAVEN. |
| |
|
|
|
| 1. |
Geef een formule voor onderstaande
exponentiŽle tabellen. Toon eerst aan dat het gaat om een exponentieel
verband. |
| |
|
|
|
| |
a. |
| x |
0,9 |
4,5 |
6,2 |
8,9 |
12,1 |
13,4 |
| y |
8,5 |
70 |
191 |
935 |
6134 |
13171 |
|
| |
|
|
|
| |
b. |
| x |
-8,7 |
-7,6 |
-4,4 |
-3,5 |
-2,1 |
-1,8 |
| y |
5,00 |
4,45 |
3,18 |
2,89 |
2,50 |
2,42 |
|
| |
|
|
|
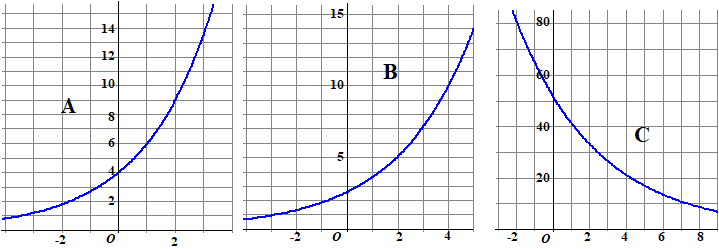
| 2. |
Hieronder staan 3 grafieken van de
vorm y = B ē gx
Bepaal van elk van deze grafieken zo goed mogelijk de waarden van
B en g. |
| |
|
|
|
|
 |
| |
|
|
|
| 3. |
De dikte van de ozonlaag neemt
de laatste tijd onrustbarend af, vooral door het gebruik van drijfgassen
in spuitbussen. Metingen leverden de volgende tabel: |
| |
|
|
|
| |
| jaar |
dikte in m |
1980
1981
1982
1983 |
1486
1441
1398
1356 |
|
|
| jaar |
dikte in m |
1984
1985
1986
1987 |
1316
1276
1238
1201 |
|
|
| |
|
|
|
| |
a. |
Bewijs dat deze afname exponentieel is en
geef een formule voor de dikte (D) als functie van de tijd t (in
jaren met t = 0 in 1980) |
| |
|
|
|
| |
b. |
In hoeveel tijd halveert de dikte van de
ozonlaag? |
| |
|
|
|
| 4. |
Het stralingsniveau (S) op een
bepaalde plaats direct na het inslaan van een lange-afstands raket met
nucleaire kop hangt af van de afstand (a in km) tot de plaats van
inslag. Metingen leverden de volgende tabel: |
| |
|
|
|
| |
| stralingsniveau (S) |
161000 |
108000 |
32600 |
12000 |
4400 |
| afstand (a) |
2 |
4 |
10 |
15 |
20 |
|
| |
|
|
|
| |
Er blijkt te gelden S(a)
= 240000 ē 0,8a |
| |
|
|
|
| |
a. |
Leg duidelijk uit hoe deze formule uit
bovenstaande tabel valt af te leiden. Toon daarbij eerst aan dat
het hier gaat om exponentiŽle afname. |
| |
|
|
|
| |
b. |
De voor een mens dodelijke dosis straling is 200
of meer. Tot welke afstand vanaf de plaats van inslag zullen er direct doden gaan
vallen? |
| |
|
|
|
| 5. |
Examenopgave HAVO Wiskunde A,
2022-I
In 2015 was het jaargemiddelde van de CO2-concentratie in de
lucht 400,8 ppm (parts per
million: het aantal CO2-deeltjes per miljoen luchtdeeltjes)
Wereldwijd
worden er afspraken gemaakt met als doel de CO2-concentratie
omlaag te brengen. Veronderstel dat het inderdaad lukt om de CO2-concentratie
na 2015 zodanig te laten dalen dat het jaargemiddelde in 2050 nog
maar 350 ppm is. Dan kan er bijvoorbeeld sprake zijn van afname
volgens
- een lineair verband of
- een exponentieel verband.
In beide gevallen is het jaargemiddelde in 2015 gelijk en is ook het
jaargemiddelde in 2050 gelijk. Echter, een CO2-concentratie
van bijvoorbeeld 375 ppm wordt in het ene geval op een eerder moment
bereikt dan in het andere geval.
Leg uit, zonder
berekeningen te geven, in welk van de twee genoemde gevallen de CO2-concentratie
het eerst de waarde 375 ppm bereikt. |
| |
|
|
|
 |
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|