| |
© h.hofstede (h.hofstede@hogeland.nl)
|
|
 |
|
          |
| |
|
Wortels |
| |
|
|
|
Eerst even iets over de notatie
met wortels.
Ook met wortels zijn blokjes mogelijk. Dat kun je op twee manieren
noteren.
Op de eerste plaats kun je natuurlijk haakjes gebruiken: dat maakt er
automatisch één geheel van. Maar je kunt ook een streep boven het
wortelteken doortrekken. Dit betekent precies hetzelfde: |
| |
|
|
|
|
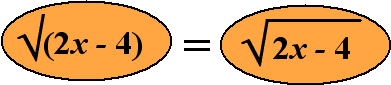 |
| |
|
|
|
| Die (2x
- 4) hoort in zijn geheel bij die
wortel. |
| |
|
|
|
Wat is eigenlijk een wortel?
In de tweede klas heb je (hoop ik) geleerd dat wortels het omgekeerde
van kwadraten zijn.
(kwadraat was trouwens: getal keer zichzelf doen)
Zo geldt dat: |
|
√16 = 4 want 42 = 16
√225 = 15 want 152 = 225
√3 ≈ 1,7 want 1,72 ≈ 3
122 = 144 dus √144 = 12
0,82 = 0,64 dus √0,64 = 0,8 |
| |
|
|
|
| Dat tekentje ≈
betekent "is ongeveer gelijk aan". |
| |
|
|
|
|
Als je de wortel van een getal in het
kwadraat doet, dan krijg je het getal zélf.
(√x)2 =
x |
|
| |
|
|
|
Wil je dus graag
weten hoe groot √300 is dan zoek je een getal dat keer zichzelf 300
oplevert. Dat is lastig te vinden, het zit ergens tussen de 17 en 18
want 172 = 289 en 182 = 324.
Gelukkig heeft je GR een knop om direct wortels te berekenen. Zoek hem
zelf maar op.Wortels
vereenvoudigen.
Er is eigenlijk maar één belangrijke
regel om wortels te vereenvoudigen, en dat is: |
| |
|
|
|
|
|
| Bewijs!! |
|
| |
Je hoeft bij wiskunde
A eigenlijk geen bewijzen te kennen, maar ik wil je toch een keer laten
zien hoe zoiets in z'n werk gaat.
Stel dat je wilt weten hoe je √3 √15 anders kunt schrijven
Begin met (√3 √15)2
een kwadraat is "keer zichzelf" dus (√3 √15)2 = (√3
√15) (√3 √15)
maar dat is één blokje, dus die haakjes kunnen weg: (√3 √15)2
= √3 √15 √3 √15
je kunt nu √3 √3 en √15 √15 uitrekenen: dat is 3
en 15, dus (√3 √15)2 = 3 15
hier staat nu eigenlijk (.....)2 = 3 15
maar dan is (.....) gelijk aan √(3 15)
dus √3 √15 = √(3 15) |
| Bewezen !!! |
| |
|
Bedenk dat deze regel
zowel van links naar recht als van recht naar links gebruikt mag worden.
Er staat eigenlijk √a √b =
√(ab) en √(ab) =
√a √b
Dat "de andere kant op" kun je ook gebruiken om wortels
te vereenvoudigen. |
| |
Vier Voorbeeldjes daarvan:
√80 = √(16 5) = √16 √5 = 4√5
√(4x) = √4 √x = 2√x
√(144p2) = √144 √p2 = 12p
√(25a) + √(9a) = √25 √a + √9
√a = 5√a + 3√a = 8√a |
|
| |
|
|
|
Er is nog een tweede
regel voor het rekenen met wortels, maar die komt niet zo vaak voor.
Dat is deze: |
|
|
| |
|
|
|
| Misschien onthoud je
het beter in woorden: |
| |
|
|
|
|
Bij vermenigvuldigen en
delen mag je wortels splitsen of samennemen. |
|
| |
|
|
|
Bedenk goed dat dat
bij optellen en aftrekken dus NIET mag!!!! (het zelfde zullen we
later ook bij breuken zien)
Bij optellen en aftrekken kun je niet vereenvoudigen.
Daar moet je afblijven.
Dat moet je gewoon laten staan.
En toch gaat dat vaak fout. Ik snap dat wel, dat komt doordat we zoveel
met haakjes hebben geoefend. Daar moesten we steeds boogjes maken om ze
weg te werken. Geef toe, dit is wel erg aantrekkelijk om met elkaar te
vergelijken: |
| |
|
|
|
|
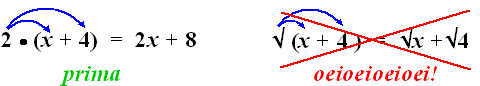 |
| |
|
|
|
| |
|
|
|
| |
|
|
|
OPGAVEN. |
| |
|
|
|
| 1. |
GOED of FOUT? |
| |
|
|
|
| |
a. |
√(36q) = 6√q |
e. |
√t + √t
= √(2t) |
| |
|
|
|
|
| |
b. |
√(9 + s) = 3 + √s |
f. |
√(4 + x) √(4
+ x) = 16 + x |
| |
|
|
|
|
| |
c. |
√(x) √(x
+ 1) = √(x2 + 1) |
g. |
√(b + b
+ 2b) = 2√b |
| |
|
|
|
|
| |
d. |
√(M) + √(2M)
= √(3M) |
h. |
√(9x) - √(4x)
- √(x) = 0 |
| |
|
|
|
|
| 2. |
Schrijf de volgende
uitdrukkingen zo eenvoudig mogelijk: |
| |
|
|
|
| |
a. |
√(2y) √(8y) |
d. |
√(b + b + b + b) |
| |
|
|
|
|
| |
b. |
√(16a) + √(4a) |
e. |
√(9a2) + 2a |
| |
|
|
|
|
| |
c. |
√45 + 2√5 |
f. |
√(20p + 5p) |
| |
|
|
|
| 3. |
Kleine Laurens groeit
als een wortel!
Letterlijk in dit geval, want zijn ouders hebben elke maand vanaf zijn
geboorte zijn lengte gemeten en kwamen tot de volgende formule:
L = 20,3 (0,2√(5t)
+ 2,6)Daarin is L de lengte in cm en t
de tijd in maanden vanaf zijn geboorte. |
| |
|
|
|
| |
a. |
Hoe lang was Laurens bij zijn
geboorte? |
| |
|
|
|
| |
b. |
Wanneer was Laurens 1
meter lang? |
| |
|
|
|
| |
c. |
Je kunt de formule
voor L ook schrijven als L = a + b√t
Daarin zijn a en b twee getallen
Bereken deze getallen in twee decimalen nauwkeurig. |
| |
|
|
|
| 4. |
Als je een voorwerp van een toren
met hoogte 51 meter naar beneden laat vallen, dan geldt voor de
valtijd t (met t in seconden en t = 0 op
het moment van loslaten) en de hoogte h (in
meters) de volgende formule:
t = 4,1 √(2,55 - 0,05h)
|
| |
|
|
|
| |
a. |
Na hoeveel seconden
is het voorwerp op de grond? |
| |
|
|
| |
b. |
Hoeveel meter valt
het voorwerp in de derde seconde?
Wat was in die seconde de gemiddelde snelheid in km/uur? |
| |
|
|
|
| |
c. |
Je kunt de formule
ook schrijven als t = √(a -
bh)
Daarin zijn a en b twee getallen.
Bereken deze getallen in twee decimalen nauwkeurig. |
| |
|
|
|
 |
|
|
|
© h.hofstede (h.hofstede@hogeland.nl)
|