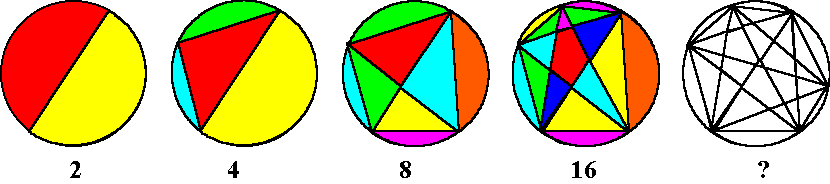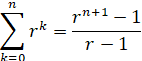volledige inductie

© h.hofstede (h.hofstede@hogeland.nl)

Volledige Inductie.

Proof By Induction:
1. Obtain a large power transformer
2. Find someone who does not believe your theorem
3. Get him to hold the terminals of your generator
4. Apply 25000 Volts AC to the generator
5. Repeat step 4 until he agrees with the theorem

Een bewijs via volledige inductie is eigenlijk een oneindige rij dominostenen die omvalt.
Stel dat je van een perfect opgestelde rij dominostenen bij elke steen zeker weet dat áls die omvalt, dat dan ook de volgende omvalt.....
Volgens mij weet je dan ook zeker dat, als je de eerste omgooit, de hele rij zal vallen.
Ja toch?

Nou, dat heb je het principe van de volledige inductie begrepen.

Als je een eigenschap met een inductiebewijs wilt bewijzen dan gaat dat altijd in twee stappen:

stap 1.

Laat zien dat de eigenschap voor het eerste geval geldt.

stap 2.

Laat zien dat, als de eigenschap voor een geval geldt, dat hij dan ook voor het volgende geval geldt.

Stap 1 brengt de boel op gang, en stap 2 zorgt dat de eigenschap voor geval 1, dan 2, dan 3, dan 4, ...... geldt.
Ofwel: de dominoreeks valt! De eigenschap geldt altijd!!!
q.e.d.

Voorbeeld 1: een formule van Gauss.

Toon aan dat: 1 + 2 + 3 + ... + n = ¹/₂ • n • (n + 1)

stap 1:

de stelling geldt voor n = 1, kijk maar: 1 = ¹/₂ • 1 • 2

stap 2:

stel dat de stelling klopt voor een bepaalde n. dan geldt dus 1 + 2 + ... + n = ¹/₂ • n • (n + 1)
het volgende geval is dan n + 1.
Het gaat dan om 1 + 2 + ... + n + (n + 1) en we hopen dat dat gelijk is aan ¹/₂ • (n + 1) • (n + 2)

We kunnen nu alles van 1 tm n vervangen door die formule, immers die klopte voor n:
1 + 2 + ... + n + (n + 1) = ¹/₂ • n • (n + 1) + (n + 1)
1 + 2 + ... + n + (n + 1) = ¹/₂ • n • (n + 1) + ¹/₂ • 2 • (n + 1)
1 + 2 + ... + n + (n + 1) = ¹/₂ • (n + 1) • (n + 2)
En daar staat dat de stelling dan ook voor n + 1 geldt.
De domino's doen de rest.
q.e.d.

Kijk uit dat je de volgende stap wel echt bewijst. Dat je je aardig kunt vergissen blijkt misschien wel uit de volgende serie. We gaan een cirkel verdelen in segmenten door een aantal punten op de omtrek met elkaar te verbinden. Als we steeds een punt toevoegen groeit het aantal segmenten.
Hieronder staat het maximaal aantal segmenten

Je denkt uiteraard "bewezen" te hebben dat de laatste cirkel wel 32 segmenten zal bevatten.
Maar is dat wel zo? ????


OPGAVEN

1.	a.	Toon aan dat 8ⁿ - 3ⁿ altijd deelbaar is door 5. Maak daarbij gebruik van de uitdrukking 8^{n + 1} - 3 • 8ⁿ + 3 • 8ⁿ - 3^{n + 1}

	b.	Toon aan dat voor elk natuurlijk getal n geldt dat 15ⁿ - 1 deelbaar is door 7.

	c.	Toon aan dat voor elk natuurlijk getal 9n - 1 deelbaar is door 8

	d.	Toon aan dat voor elk natuurlijk getal geldt dat 2^{n + 2} + 3^{n+ 1} deelbaar is door 7

2.	Toon aan dat de afgeleide van y = xⁿ gelijk is aan y = n × xⁿ^{- 1}

3.	a.	Toon aan dat 1 + 3 + 5 + 7 + ..... + 2n - 1 = n²

	b.	Toon aan dat geldt: 1³ + 2³ + 3³ + ... + n³ = ¹/₄ × n² × (n + 1)²

	c.	Toon aan dat 1² + 2² + 3² + ... + n² = ¹/₆ × n × (n + 1) ∙ (2n + 1)

4.	Voor de som van een meetkundige rij geldt:

	Toon dat aan.

5.	a.	Toon aan dat (1 + h)ⁿ ³ 1 + nh (voor h > -1 en n geheel).

	b.	Toon aan dat voor n ³ 4 geldt dat n! > 2ⁿ

6.	Het puzzeltje hiernaast heet de `Torens van Hanoi`. Het bestaat uit drie houten pinnen met een aantal (in de figuur 8) schijven met een gat in het midden die op de pinnen gelegd kunnen worden. De schijven variëren van groot naar klein. De bedoeling van de puzzel is de hele toren van pin1 naar pin 3 te verplaatsen. Dat moet schijf voor schijf gebeuren, en daarbij is de enige regel: "Er mag nooit een grotere schijf bovenop een kleinere liggen" .

	Toon aan dat er 2ⁿ - 1 zetten nodig zijn om een toren van Hanoi van n schijven te verplaatsen.

7.	Alle inwoners van Warffum zijn even oud? Als Warffum 1 inwoner heeft, dan is die uiteraard even oud Stel dat, als Warffum n inwoners heeft, die allemaal even oud zijn. Als er nu een nieuwe inwoner bij komt doen we het volgende: We sturen even een andere inwoner weg. Op dat moment heeft Warffum weer n inwoners, en die zijn volgens onze aanname even oud. Dat betekent dat de nieuwe inwoner dezelfde leeftijd heeft als alle anderen die er al woonden. De weggestuurde inwoner mag terugkomen, en dus heeft Warffum nu n +1 inwoners die even oud zijn. Daaruit volgt de stelling. Wat is hier fout gegaam?

8.	Stel we hebben een oneven aantal mensen die we elk een goed gevuld waterpistool geven. Daarna zetten we deze mensen met z'n allen in een grasveld. We zorgen er daarbij voor dat hun afstanden verschillen. Voor elke persoon zijn de afstanden van alle anderen tot hem of haar verschillend. Als we een teken geven mogen ze allemaal beginnen te schieten. Het blijkt dat iedereen begint te schieten op degene die het dichtst bij hem staat. Het blijkt dat er dan altijd iemand is die helemaal droog blijft.....

	a.	Toon deze stelling aan voor n = 3

	b.	Stel dat de stelling geldt voor bepaalde n. Voeg nu 2 mensen A en B toe. Kijk nu naar de twee mensen die het dichtst bij elkaar staan, en laat die even weg uit de groep. Wat kun je concluderen?

9.	Stelling: "Een willekeurig aantal vierkanten kun je altijd zó in stukken knippen dat van al deze stukken samen één groot nieuw vierkant gelegd kan worden". Met twee vierkanten kan het. Kijk maar:



	Toon daarmee aan dat het bij een willekeurig aantal vierkanten ook kan.

10.	Toon aan dat voor elk natuurlijk getal n⁵ - n deelbaar is door 10.