|
||||||
 |
||||||
| Van toenamendiagram naar grafiek. | ||||||
| Deze les gaan we
bekijken hoe je een grafiek kunt schetsen als je een toenamendiagram
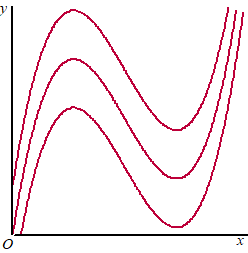
hebt. Nou daar kunnen we kort over zijn: Dat kan niet!! Waarom niet? Daar zijn twee redenen voor. Reden 1. Een toenamendiagram zegt alleen maar hoeveel een grafiek verandert en niet hoe hoog de grafiek is. De volgende grafieken hebben allemaal exact hetzelfde toenamendiagram, ze zijn alleen verticaal ten opzichte van elkaar verschoven. |
||||||
|
|
||||||
| Om een grafiek te schetsen zul je toch ergens een vast punt van die grafiek moeten hebben. | ||||||
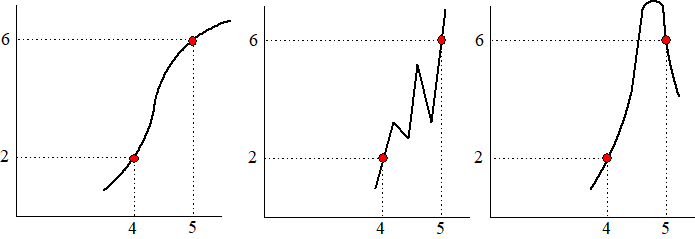
| Reden 2. Als je weet hoeveel een grafiek tussen twee x-waarden is toegenomen of afgenomen geeft dat alleen het totaal resultaat tussen die twee x-en, en het zegt niets over de manier waarop dat tot stand is gekomen. De volgende grafieken hebben tussen x = 4 en x = 5 allemaal een toename van 4. |
||||||
|
|
||||||
| Dat is de reden dat er in opgaven steeds staat "teken een mogelijke grafiek" | ||||||
| Het tekenen. | ||||||
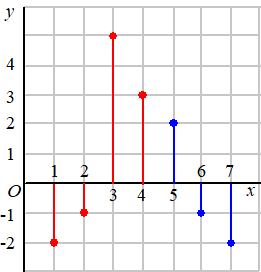
| Neem het
toenamendiagram hiernaast en stel dat je weet dat de grafiek door het
punt (4, 6) gaat. Dan kun je aan die drie blauwe stokjes van links naar rechts zien: tussen 4 en 5 stijgt de grafiek 2, dus hij gaat door (5, 8) tussen 5 en 6 daalt de grafiek 1, dus hij gaat door (6, 7) tussen 6 en 7 daalt de grafiek 2, dus hij gaat door (7, 5) Bedenk goed dat zo'n stokje dus zegt wat er met de grafiek gebeurd is vanaf het vorige punt. Dan kun je aan die rode stokjes van rechts naar links zien: tussen 3 en 4 is de grafiek 3 gestegen, dus hij ging door (3, 3) tussen 2 en 3 is de grafiek 5 gestegen dus hij ging door (2, -2) tussen 1 en 2 is de grafiek 1 gedaald, dus hij ging door (1, -1) tussen 0 en 1 is de grafiek 2 gedaald, dus hij ging door (0, 1) |
|
|||||
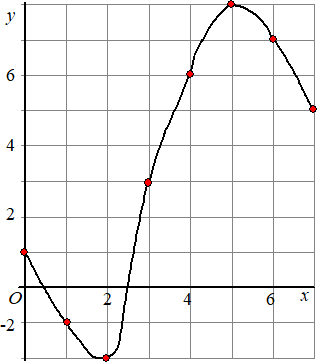
| Dat geeft de punten (0, 1)(1, -1)(2, -2)(3, 3)(4, 6)(5, 8)(6, 7)(7, 5). Hieronder zie je die punten met een mogelijke grafiek erdoor. | ||||||
|
|
||||||
|
|
||||||
| OPGAVEN. | ||||||
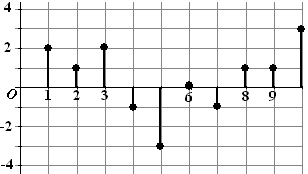
| 1. | Hiernaast staat het toenamendiagram
van een functie f. Schets een mogelijke grafiek voor deze functie, als je weet dat hij door (5,12) gaat.
|
 |
||||
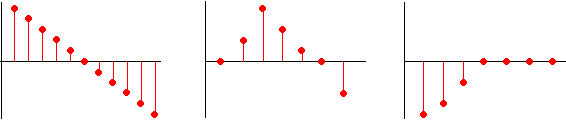
| 2. | Schets mogelijke grafieken bij de toenamendiagrammen hieronder. | |||||
|
|
||||||
| 3. | examenvraagstuk HAVO wiskunde
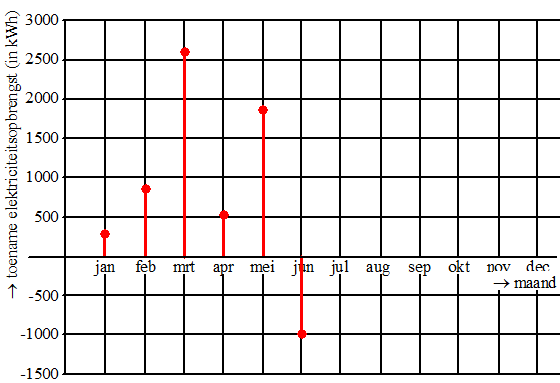
B, 2017-II Een school heeft een grote hoeveelheid zonnepanelen op het dak staan. In het jaar 2011 was de elektriciteitsopbrengst van deze zonnepanelen in totaal 45000 kWh, waarvan 520 kWh in de maand december. In het toenamediagram in de figuur zijn de gegevens van het eerste halfjaar van 2012 verwerkt. |
|||||
|
|
||||||
|
Uiteindelijk bleek dat in het jaar 2012 5000 kWh
minder elektriciteit werd geproduceerd dan in 2011. Bereken hoeveel elektriciteit er in het tweede halfjaar van 2012 is geproduceerd. Geef je eindantwoord in honderden kWh nauwkeurig. |
||||||
| 4. |
Meneer de
Groot heeft op 5 september aandelen gekocht. Zijn aandelenpakket
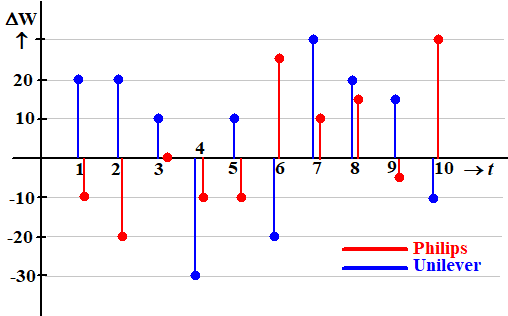
bestaat uit 20 aandelen Unilever en 40 aandelen Philips. Hieronder zie je in één figuur twee toenamendiagrammen van de waarde van deze aandelen met t = 0 op 1 september (t in dagen). De toenamen zijn in eurocenten. |
|||||
|
|
||||||
| a. | Wat was de waarde van een aandeel Philips op 1 september? | |||||
| b. | Hoeveel procent is de totale waarde van het pakket van meneer de Groot toegenomen op 10 september? | |||||
 |
||||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
||||||
