© h.hofstede (h.hofstede@hogeland.nl)

Recht Evenredig  
Probeer eerst zelf eens een formule te maken met de letters die tussen haakjes staan bij de volgende "verhaaltjes":
1. Het inkomen (I)  van de penningmeester van een club en het aantal leden (L) als voor iedereen de contributie gelijk is aan  €45,-.
2. Op een toets kun je 20 punten halen en je cijfer (C) is de helft van je aantal punten (P).
3. De kosten (K)  voor de flessen wijn die ik koop en het aantal gekochte flessen (A), als elke fles €6,- kost.
4. De omtrek (O)  van een vierkant en de lengte (L) van een zijde.
5. Jolanda krijgt in een sponsorloop €3,40 per rondje dat zij loopt, en ze loopt  (n) rondjes. 
Haar totale opbrengst is (O).
 
Ikzelf zou eigenlijk automatisch de formules hiernaast verzinnen... ik hoop jij ook....

Zie je de rode draad?

Deze formules zien er allemaal uit als: y = a • x   waarbij a dan elke keer een constant getal is (dat bij het verhaaltje hoort).
Wiskundigen (en jij dus vanaf nu ook) zeggen in zulke gevallen:

ANTWOORDEN
1.  I = 45 • L
2.  C = 0,5 • P
3.  K = 6 • A
4.  O = 4 • L
5.  O = 3,40 • n

"y is recht evenredig met x"
y = a • x
Dat constante getal a is een erg belangrijk getal voor de rest van dit hoofdstuk.
Het zegt eigenlijk hoeveel y toeneemt als x eentje toeneemt.
   

a  is de toename van y  "per  x"

Zelf formules maken
Dat legt het handigst uit met twee voorbeelden;

voorbeeld 1.
Ik ga op vakantie op een camping staan, en dat kost me een vast bedrag per nacht.
Het blijkt dat ik voor 8 nachten  € 264 moet betalen.
Stel een formule op voor  N = aantal nachten en   K = totale kosten.

oplossing: 
Het getal a is hoeveel het per nacht kost.
Als 8 nachten  € 264 kosten dan is dat per nacht  264/8 = 33
De formule wordt dan  K = 33 • N
voorbeeld 2.
De volgende tabel hoort bij een recht-evenredig verband. Maak daar een formule voor..
 x 4,3 8,1 15,7 22,5 32,0
 y 22,36 42,12 81,64 117,00 166,40
oplossing: 
Je ziet dat, als x = 4,3 is, dan is y = 22,36
Per x is dat een toename van  22,36/4,3 = 5,2
Dus a = 5,2
De formule wordt dan  y = 5,2 • x
   
De toename van y en de toename van x
   
De tabel van dat laatste voorbeeldje is nog best interessant.
Kijk eens wat er gebeurt als x toeneemt van  4,3 naar 8,1 : dat is een toename van  3,8
Dan neemt y toe van  22,36 naar 42,12 :  dat is een toename van 19,76
Dus als x met 3,8 toeneemt dan neemt y met 19,76 toe.
PER x  is dat een toename van y van  19,76/3,8 = 5,2
Hé!!!! Dat is wéér a die we gevonden hadden

Is dat toeval?

Nee natuurlijk niet!!!

Die a was immers de toename van y per x......
Kijk maar;  het klopt overal in de tabel:
(81,64 - 42,12)/(15,6 - 8,1) = 5,2
(117,00 - 81,64)/(22,5 - 15,7) = 5,2
(166,40 - 117,00)/(32,0 - 22,5) = 5,2
(117,00 - 22,36)/(22,5 - 4,3) = 5,2
en ga zo maar door......
   
Wiskundigen gebruiken voor het woord "toename" meestal de Griekse letter Δ  (dat is de D van difference = verschil). Ook bij afname noemen we het trouwens nog steeds Δ.
Daarmee zou je de volgende belangrijke formule kunnen opstellen:
   

Grafieken.
Helemaal aan het begin hadden we de volgende formules gevonden:

I = 45 • L   en   C = 0,5 • P   en   K = 6 • A   en  O = 4 • L  en   O = 3,40 • n

Hier staan de grafieken van deze formules (er is steeds een doorgetrokken lijn getekend in plaats van losse stippen)

Het valt direct op, lijkt me:  het zijn allemaal rechte lijnen die door de oorsprong gaan.
Conclusie:

De grafiek van een recht evenredig verband y = ax
is een rechte lijn door de oorsprong.
 
Ik hoop dat je dat volslagen logisch vindt:
 

Als de y bij toename van x steeds gelijkmatig toeneemt, dan gaat de grafiek elk stapje gelijkmatig  omhoog, dus wordt de grafiek
vanzelf een rechte lijn.
   
   OPGAVEN
1. Maak een formule bij de volgende recht-evenredige verbanden:
     
a. Een auto rijdt 1 op 15. Dat wil zeggen dat hij met 1 liter benzine 15 kilometer kan rijden.
1 liter benzine kost op dit moment €1,20.
Maak een formule voor het bedrag (B) dat je aan benzine kwijt bent bij een afstand van a kilometer
     
b. Als je een gewicht aan een veer hangt, dan rekt hij uit. Hoe zwaarder het gewicht, des te verder rekt de veer uit.
Bij een gewicht van 20 kilogram rekt een bepaalde veer 4 cm uit
Geef een formule voor de uitrekking (U) van deze veer bij een belasting B.
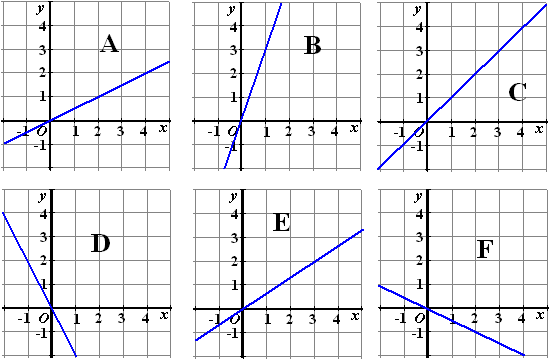
2. Van welke recht-evenredige  formules zijn dit de grafieken?

 

         
3. examenvraagstuk HAVO wiskunde A, 2015.

Geld lenen kost geld. Soms kost het heel veel geld. Vooral als je direct een paar honderd euro nodig hebt. In dit soort situaties kun je een flitslening nemen. Je leent een niet al te groot geldbedrag en betaalt dit na een korte periode terug.

Er bestaan verschillende websites waar je geld kunt lenen. Op de website flitsmoney.nl staat dat er geen rente wordt berekend. Je hoeft alleen behandelingskosten te betalen. Zie de volgende tabel.
         
 
te lenen bedrag (in euro) behandelingskosten (in euro)
100,00 25,00
250,00 62,50
300,00 75,00
375,00 93,75
         
  Als je bijvoorbeeld € 100,00 wilt lenen, krijg je dit geld binnen 10 minuten op je bankrekening. Dit bedrag moet samen met de € 25,00 behandelingskosten na 30 dagen worden terugbetaald.

Er is bij Flitsmoney een (recht) evenredig verband tussen het totaal terug te betalen bedrag en het te lenen bedrag.
Laat dit met berekeningen zien. Controleer hiervoor alle waarden in de tabel.
         
   
         

© h.hofstede (h.hofstede@hogeland.nl)