| |
© h.hofstede (h.hofstede@hogeland.nl)
|
| |
|
| Het
Ongerijmde |
Proof By Contradiction:
1. State your theorem
2. Wait for someone to disagree
3. Contradict them. |
|
|
|
|
Logische
Verantwoording.
Een bewijs uit het ongerijmde ('reductio ad
absurdum') berust op een stukje
logica.
Een bewering "als A dan B" schrijven we
wiskundig als volgt A ⇒ B
De pijl heet een implicatiepijl. (A impliceert B).
Maar hieruit volgt logisch gezien niet dat "Als B dan A".
Vergelijk: "Als het morgen regent dan blijf ik binnen"
met "Als ik morgen binnen blijf, dan regent het".
Deze
beweringen zijn duidelijk niet gelijkwaardig, want als dat wel zo was, dan zou
ik door binnen te blijven het morgen kunnen laten regenen!!
"Als het morgen regent dan blijf ik binnen" is wél gelijkwaardig
met: "Als ik morgen niet binnen blijf, dan regent het niet"
Logisch genoteerd: ¬B ⇒ ¬A (¬ betekent
"niet", dus als niet-B dan niet-A). |
|
 |
|
|
|
| |
Maar goed, ook voor de
allerbeste logicus van deze eeuw waren dit soort redeneringen te moeilijk!!!
WAAAAAT??? Zul je zeggen? Beheerste Frege deze elementaire logica-materie niet?
Of Gödel misschien? Nee... niet zeggen... was het dan Russell???
Nee, natuurlijk niet! Je mist dan de allerbeste logicus van deze eeuw.
|
Zonder twijfel is dat natuurljk..... Mister Spock!!!!
Je zult het niet geloven, maar ook deze Vulcan maakte de elementaire logica-fout
hierboven genoemd.
In een episode van STAR TREK was de Enterprise geraakt door een ionenstorm, en
de motoren waren uitgevallen. De volgende twee plaatjes speelden zich vervolgens
af tussen captain Kirk en Mr.Spock. Eerst als de motoren uit zijn, daarna als de
motoren even later weer aan gaan. Kijk en huiver.....
Brrrrr! Als de beste Logicus
ooit zo'n elementaire fout maakt dan kun je het ons gewone stervelingen
natuurlijk ook niet kwalijk nemen! Mr. Spock draait hier zomaar een bewering Als
A dan B om in Als B dan A!
Je mag een bewering als...
dan....wel omdraaien, maar alleen als je voor beide maar NIET zet!!!
Spock zou als de motoren niet aan zouden gaan, hoogstens kunnen concluderen dat Scotty er
NIET is.
Deze
"omkering-met-NIET-ervoor" geeft ineens de mogelijkheid een
bewering te bewijzen! Stel dat ik bewering A wil bewijzen. Dan laat ik zien dat
uit ¬A een foute bewering volgt.
¬A ⇒ B is immers gelijkwaardig met ¬B
⇒ ¬¬A = A. Dus
als ik zeker weet dat B fout is, dan is ¬B waar, en dus A ook. Ik heb zo'n
redenering hierboven als stiekem gebruikt, nl. naast het varkentje hierboven
("Deze beweringen zijn...") en je geloofde het direct natuurlijk!.
Een bewijs uit het ongerijmde klinkt altijd als volgt:
"Stel dat bewering A NIET waar zou zijn. Dan volgt daar B uit. Maar
omdat we van B weten dat het niet waar is, moet A dus wel waar zijn".
Beroemd Voorbeeldje:
Stevin's Hellend Vlak
De "Beghinselen der
Weeghconst" van Simon Stevin werd in 1586 uitgegeven (in één
band met "De Weeghdaet", "De Beghinselen des Waterwichts",
en een "Anhang" en in 1605 kwam er nog een "Byvough"). Het
behandelt de theorie van krachten die elkaar in evenwicht houden. Zoiets als wat
wij nu statica zouden noemen.
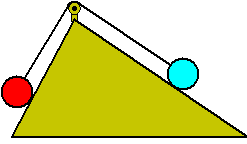
Een klassiek en antiek probleem was : "Evenwicht op een hellend vlak"
Twee bollen, verbonden door een touw via een
katrol hangen rusten op twee vlakken met verschillende hellingshoeken.
(het touw en de katrol zijn gewichtloos en alles beweegt wrijvingsloos
uiteraard)
Wanneer is er evenwicht?
Stevin zegt in zijn "Voorstel 19":
|
| Ghelijck des driehoucx rechter sijde
tot de slincker, also t'staltwicht
des cloots op de slincker sijde, tottet staltwicht des cloots
op de rechter sijde. |
|
|
|
|
Zo. Daar kun je 't mee doen.
Hij bedoelt natuurlijk te zeggen dat er evenwicht is als de verhouding van de
gewichten gelijk is aan de verhouding van de lengte van de zijden waarop
zij rusten.
Als bijv. de rechterzijde dubbel zo lang is als de linkerzijde, dan moet
voor evenwicht het blauwe gewicht ook dubbel zo groot zijn als het
rode. |
|
|
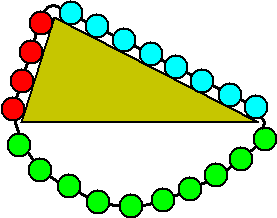
| Stevin geeft als bewijs het beroemde 'clootcrans-bewijs'
met de "bollenkrans" hiernaast. Hij was er zó mee in zijn
nopjes dat de figuur hiernaast zelfs zijn logo is geworden..
STEL dat er géén evenwicht is (het ongerijmde)....
Dan zou de ketting gaan bewegen (geen wrijving!)
Maar in die nieuwe situatie zou er nog steeds geen evenwicht zijn, dus de
ketting zou alsmaar door blijven bewegen.
We hebben een Perpetuüm Mobile!!
|
| "...ende de clooten sullen
uyt haer selven een eeuwich roersel
maken, t'welck valsch is". |
|
|
Er moet wel evenwicht zijn.
(Het aantal bollen is uiteraard evenredig met de lengte van de zijde). |
|
Contra-Positief
Er is een tweede soort "bewijs uit het ongerijmde"
die erg veel lijkt op de hierboven genoemde, maar er is een subtiel verschil. We
wilden hierboven bewering A bewijzen, en begonnen dan met ¬A
en hoopten dat daaruit "iets" tegenstrijdigs zou volgen. Het was
alleen niet direct duidelijk wat dat "iets" dan zou moeten zijn.
Het kan ook
directer.
Zo'n bewijs heet "Contra-positief"
, en gaat als volgt:
We zagen al dat uit A ⇒
B volgt ¬B ⇒
¬A.
Dus als we kunnen bewijzen dat uit ¬B volgt dat ¬A, dan hebben
we de bewering A ⇒
B ook bewezen. Let wel: we bewijzen dus niet een bewering A, maar
een bewering van de vorm "Als A dan B". We zeggen niets
over het al of niet waar zijn van A, alleen over de gevolgtrekking
(als A waar zou zijn, dan is B ook waar). |
Het doel is hier steeds
duidelijk: probeer ¬A aan te tonen.
"Ho stop eens," hoor ik je al zeggen. "Hierboven bij de
ongerijmde bewijzen stond óók een als... dan... bewering (namelijk de
vierde)". Toch was de aanpak daar anders. Kijk maar:
A = "in een driehoek geldt a2 + b2
= c2"
B = "de driehoek heeft een rechte hoek".
Contra-positief gaat het zó:
Neem een driehoek zonder rechte hoek, en probeer te bewijzen dat dan a2
+ b2 ≠
c2
In symbolen: ¬B ⇒
¬A.
Uit het ongerijmde gaat het zó:
Neem een driehoek zonder rechte hoek waarin geldt a2 + b2
= c2 en probeer op flauwekul uit te komen.
In symbolen: (¬B én A) ⇒
onzin (maar wélke onzin is nog onbekend)
Voorbeelden van contra-positieve
bewijzen:
|
|
Gedachte-Experimenten.
Nauw verbonden met de bewijzen uit het ongerijmde zijn de zogenaamde
"Gedachte-experimenten".
Het gaat hier meest om natuurkundige dingen die bewezen worden (af en toe
zelfs filosofische zaken). De experimenten beginnen bijna allemaal met
STEL DAT... en dan volgt er een experiment dat eindigt met met onmogelijke uitkomsten.
Hierboven zagen we al een voorbeeld: het Clootcrans-bewijs van Stevin.
Het allerberoemdste gedachte-experiment is dat van Gallileï.
Rond de tijd van Gallileï was het de algemene opvatting (nog afkomstig van
de tirannie van Aristoteles) dat zware voorwerpen sneller vallen dan
lichte voorwerpen. Het verhaal gaat dat Gallileï vanaf de toren van Pisa
verschillende voorwerpen liet vallen om deze theorie te testen. Maar dat
is waarschijnlijk nooit gebeurd. Gallileï had dat niet nodig ook; hij koos
een veel mooiere methode: het gedachte-experiment. |
Stel dat een zwaar object sneller valt dan een licht object (zoals
Aristoteles beweerde).
Wat zou er dan gebeuren als we een licht en een zwaar object aan elkaar
binden?
Het zware object valt sneller en zal dus door het lichtere object
tegengehouden worden. Dus de combinatie van beiden zal minder snel vallen
dan het zware object alleen.
Maar de combinatie van beiden kun je ook zien als één nog zwaarder
object, en dan zou het juist sneller moeten vallen!
AHA! een tegenstrijdigheid. Daar heb je het bewijs uit het
ongerijmde; we zijn op onzin uitgekomen.
De enige manier om deze onzin op te lossen is te stellen dat alle
drie de objecten even snel vallen.
Q.E.D. |
 |
|
|
|
|
|
|
|
|
|
|