| "Omgekeerd
Pythagoras" |
|
|
Immers als A is "de
driehoek is recht" en B is "a2
+ b2 = c2" , dan zegt
de stelling van Pythagoras dat A ⇒
B.
Deze stelling hier beweert echter B ⇒
A.
Bewijzen uit het ongerijmde zijn erg vaak geschikt om zulke
omgekeerde stellingen te bewijzen.
Laten we maar eens beginnen aan te nemen dat we een driehoek
hebben gevonden waarin a2 + b2
= c2 geldt, maar die NIET rechthoekig is.
Dan zijn er twee mogelijkheden: de hoek bij C is stomp of
scherp.
Dat geeft de volgende twee figuren, elk met een gevolgtrekking
eronder. |
|
|
 |
 |
|
|
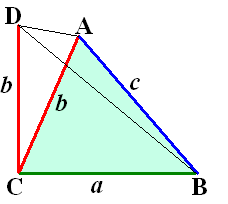
Teken CD loodrecht op AB met
lengte b.
Dan geldt BD2 = a2 + b2
= c2
Dus BD = c
Dus de driehoeken ACD en ABC zijn gelijkbenig.
Dan zijn hun basishoeken gelijk.
Dus ∠CDA = ∠CAD en ∠BDA = ∠DAB
Voor de hoeken geldt dan:
BDA < CDA = CAD < DAB
|
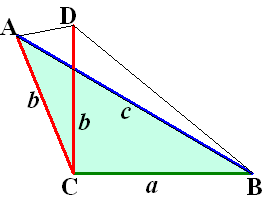
Teken CD loodrecht op AB met
lengte b.
Dan geldt BD2 = a2 + b2
= c2
Dus BD = c
Dus de driehoeken ACD en ABC zijn gelijkbenig.
Dan zijn hun basishoeken gelijk.
Dus ∠CDA = ∠CAD en ∠BDA = ∠DAB
Voor de hoeken geldt dan:
DAB < CAD = CDA < BDA |
|
|
Beide gevallen leiden tot een
onwaarheid, dus de oorspronkelijke aanname kan niet kloppen.
Daarmee is de stelling bewezen. |
|
|
|
|
|
|
|
|