| x3
+ x + 1 = 0 heeft geen rationale oplossingen |
|
|
Het begint (uiteraard) als
volgt: "Stel dat de vergelijking wél een rationale
oplossing heeft"
Laten we deze oplossing p/q stellen, met p
en q gehele getallen, en laten we aannemen dat de breuk p/q
niet verder te vereenvoudigen is. |
|
|
| p/q invullen in de
vergelijking en dan vermenigvuldigen met q3
geeft:
|
| En nu gaan we gebruik maken van het oneven of
even zijn van p en q. Daarvoor maken we gebruik
van de twee tabelletjes hiernaast: een opteltabel en een
vermenigvuldigtabel voor oneven (o) en even (e)
getallen. |
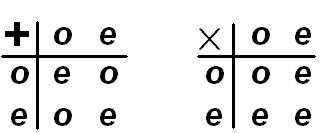 |
| Nu zijn er vier mogelijkheden voor p en q
en de vergelijking: |
|
|
|
- p is oneven en q ook. Dan staat er in de
vergelijking o3 + oo2
+ o3 = 0 ⇒
o + o + o = 0 ⇒
o = 0 en dat laatste klopt niet, want 0 is even.
- p is oneven en q is even. Dan staat
er o3 + oe2 + e3
= 0 ⇒ o + e + e =
0 ⇒ o = 0 alweer fout!
- p is even en q is oneven. Dan staat
er e3 + eo2 + o3
= 0 ⇒ e + e + o = 0
⇒ o = 0 alweer fout!
- p en q zijn even. Maar dat kan niet, want
p/q was niet te
vereenvoudigen.
|
Kortom: alle mogelijkheden leiden
tot iets dat niet klopt.
De enige mogelijke conclusie is dat de vergelijking geen
rationale oplossingen kan hebben. |