|
|
 |
|
Verschilrijen. |
©
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
Ik weet niet hoe het met jou is,
maar als ik bij een IQ test of zo een rij getallen zie, en ik moet de
volgende ervan proberen te raden, dan kijk ik eigenlijk meteen naar de
verschillen tussen de getallen. Of er regelmaat zit in hoeveel erbij
komt of vanaf gaat.
Neem de volgende rij:
| |
| 4 - 6 - 10 - 16 - 24 - 34 - 46 - .... |
| |
Als je een beetje ervaring met regelmaat in rijen hebt, dan zie je
meteen dat de verschillen van de getallen in deze rij
gelijk zijn aan 2 - 4 - 6 - 8 - 10 - 12 - ....
Dus de volgende getallen zullen zijn 60 - 76 - 94 - .... enz.
Laten we eerst even wat notatie zaken afspreken.
Δun betekent
"hoeveel erbij is gekomen om un te krijgen vanuit
de vorige un-1"
Ofwel in formule:
|
| Als je de rij hierboven in een tabel zet, dan
krijg je dit:: |
| |
|
|
| n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| un |
4 |
6 |
10 |
16 |
24 |
34 |
46 |
60 |
|
Δun |
- |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
|
| |
|
|
Als je de middelste rij even
vergeet is het niet zo moeilijk een directe formule voor
Δun te maken.
De rij voor
Δun
is namelijk gewoon een rekenkundige rij. En die kennen we....
De formule daarvan is
Δun
= 2n - 2
Maar dat maakt het mogelijk een recursieformule voor un
zélf op te stellen, immers omdat
Δun = un - un - 1
geldt ook un = un-1
+
Δun
Een belangrijke eigenschap!!!!
Deze formule maakt het mogelijk om een recursieformule van een rij te
maken als we van de verschilrij een directe formule hebben. In
bovenstaand geval zou de recursievergelijking dus worden: un
= un - 1 + 2n - 2 |
| |
|
|
|
OPGAVEN |
| |
|
|
| 1. |
Geef recursievergelijkingen voor de volgende
rijen en bepaal met je GR de waarde van u20 .
De rijen beginnen steeds met u1. |
| |
|
|
|
|
| |
a. |
8 - 10 - 16
- 26 - 40 - 58 - ... |
|
| |
b. |
50 - 54 -
57 - 59 - 60 - 60 -
59 - ..... |
|
| |
c. |
0 - 1/2
- 5/6
- 13/12
- 77/60 -
87/60
- ... |
|
| |
d. |
1 - 9 - 36 -
100 - 225 - .... |
|
|
| |
|
|
|
|
| 2. |
Gegeven is de rij un
= n2 + n
Geef een formule voor de verschilrij
Δun
van deze rij. |
| |
|
|
|
|
| 3. |
Voor de verschilrij van een rij un
geldt
Δun =
1/(n - n˛)
Geef een directe
formule als u1 = 1. |
| |
|
|
|
|
| |
|
|
|
|
| 4. |
 |
| |
|
|
|
|
| |
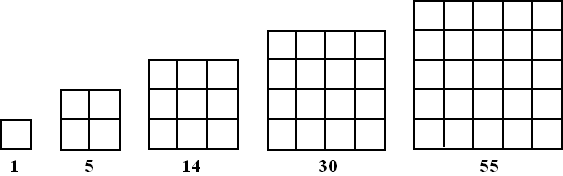
Bekijk de serie figuren hierboven.
In de eerste figuur (n = 1) zien we 1 vierkant, vandaar het getal
1 eronder.
In de tweede figuur (n = 2) zien we 4 vierkanten van 1
× 1 en ook
1 vierkant van 2 × 2. Samen is dat 5 vierkanten.
Zo staat onder elke figuur hoeveel vierkanten er te zien zijn.
Dat geeft de rij getallen un met u1 = 1 |
| |
|
|
|
|
| |
a. |
Bereken de getallen uit de verschilrij
Δun
en geef een directe formule voor
Δun |
| |
|
|
|
|
| |
b. |
Bewijs dat geldt:
un = un-1
+ n2 |
| |
|
|
|
|
| |
c. |
Hoeveel vierkanten zijn
er op een plein van 100 ×
100 vierkante tegels te
ontdekken? |
| |
|
|
|
|
| |
|
|
|
|
| 5. |
 |
| |
In het
Noord-Hollandse dorp Limmen is op 12 juni 2005
het wereldrecord bierkratten-stapelen gebracht op 63365.
De top van de uiteindelijke krattenpiramide bestond uit één
krat, de laag daaronder was 2 × 2
dus vier kratten, daaronder 3 × 3 dus negen kratten, enz.
Het totaal aantal kratten in n lagen is dus gelijk aan
Sn = 1 + 4 + 9 + ... + n2
|
| |
|
|
|
|
| |
a. |
Maak een recursieformule
voor Sn en onderzoek daarmee uit hoeveel lagen
de piramide in Limmen bestond. |
| |
|
|
|
|
| |
b. |
Op hoeveel procent van
de uiteindelijke hoogte was men toen men halverwege het aantal
kratten was? |
| |
|
|
|
|
| |
(In 2011 pakte het
Duitse plaatsje Satow het record van Limmen af, met een aantal
van 105995 kratten) |
| |
|
|
|
|
| 6. |
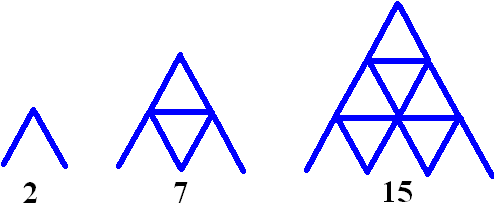
Hieronder staan
een aantal kaartenhuizen getekend.
Het eerste huis kost 2 kaarten, het tweede kost 7 kaarten, het derde
kost 15 kaarten enz.
Hoeveel kaarten kost het 50ste huis? |
| |
|
|
|
|
| |
 |
| |
|
|
|
|
| |
|
| 7. |
Gegeven
is de rij un = n2 - 3n
vn is de verschilrij van un.
Leg uit dat vn een rekenkundige rij is. |
| |
|
|
|
|
| 8. |
Als je een aantal lijnen
tekent, dan kun je daarmee een vlak in een aantal vlakdelen
verdelen.
Een interessante vraag daarbij is natuurlijk: Hoeveel
vlakdelen zijn er maximaal te maken met n rechte lijnen? |
| |
|
|
|
|
| |
a. |
Onderzoek dit probleem
door een aantal gevallen uit te proberen. |
| |
|
|
|
|
| |
Als je een
vlak in un delen hebt verdeeld door n
lijnen te tekenen, dan heeft een volgende lijn die je tekent
maximaal n nieuwe snijpunten. |
| |
|
|
|
|
| |
b. |
Leg duidelijk uit waarom
daaruit volgt dat un+1 = un
+ n |
| |
|
|
|
|
| |
c. |
Wat is het maximale
aantal vlakdelen als je 10 lijnen tekent? |
| |
|
|
|
|
| |
|
|
|
|
|
|
Polynomen |
| |
|
|
Laten we eens een eenvoudige rij
bekijken: 1 - 4 - 9 - 16 - 25 - 36 - 49 - 64 - ...
Het is, dat heb je misschien al wel gezien, de rij van de kwadraten.
Ofwel un = n2
De verschilrij daarvan is zo mogelijk nog eenvoudiger. Die staat in de
volgende tabel: |
| |
|
|
| un |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
|
Δun |
- |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
|
| |
|
|
Die laatste rij zal je wel bekend
voorkomen: de verschillen daarvan zijn allemaal gelijk aan 2.
Dus als we een volgende rij aan de tabel zouden toevoegen, waarin de
verschillen van de verschillen staan, dan geeft dat steeds 2: |
| |
|
|
| un |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
|
Δun |
- |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
|
Δ(Δun) |
- |
- |
2 |
2 |
2 |
2 |
2 |
2 |
|
| |
|
|
En nou komt het: Dat
blijkt voor elke kwadratische formule zo te zijn!!!
Het blijkt dat de formule un = an2
+ bn + c altijd als tweede verschilrij geeft 2a.
Het bewijs daarvan staat hiernaast. |
 |
| |
Van een kwadratische formule zijn de verschillen van de
verschillen constant
un = an2 + bn + c
geeft als tweede verschillen 2a. |
|
| |
|
|
|
Oké, en hoe vinden we die b
en c? |
| |
Dat is gelukkig erg
makkelijk.
Als je a hebt gevonden dan kun je van de tabel overal an2
van aftrekken.
Dat geeft een nieuwe tabel voor bn + c. Kijk maar naar het
volgende voorbeeld:
| |
| n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| un |
3 |
2 |
7 |
18 |
35 |
58 |
87 |
122 |
|
Δun |
- |
-1 |
5 |
11 |
17 |
23 |
29 |
35 |
|
Δ(Δun)
|
- |
- |
6 |
6 |
6 |
6 |
6 |
6 |
|
| |
|
Dus hieruit volgt dat 2a =
6, dus a = 3.
Maak nu een nieuwe tabel: |
| |
|
|
| n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| un |
3 |
2 |
7 |
18 |
35 |
58 |
87 |
122 |
| un - 3n2 |
3 |
-1 |
-5 |
-9 |
-13 |
-17 |
-21 |
-25 |
|
| |
|
|
Die laatste rij is het lineaire
verband un = -4n + 3
Daarmee wordt de totale formule voor un:
un = 3n2 -
4n + 3 |
| |
|
|
| |
|
|
| 9. |
Hieronder vind je een aantal rijen, steeds
beginnend bij n = 0
Zoek eerst uit van welke van deze rijen de directe formule een
kwadratische formule is, en geef vervolgens van die rijen de
directe formule.
De eerste term van de rij heet steeds u0. |
| |
|
|
|
|
| |
a. |
4 - 4 - 8 - 16 - 28 - 44 - 64 - ... |
|
| |
b. |
1 - 5 - 10 - 16 - 23 - 54 - 63 - ... |
|
| |
c. |
6 - 71 - 126 - 171 - 206 - 231 - 246
- ... |
|
| |
d. |
10 - 20 - 54 - 112 - 194 - 300 - 430
- .... |
|
| |
|
|
|
|
| |
|
|
|
|
|
Kan het ook met hogere machten?
Jazeker.
Maar dat is meer iets voor een verdieping.... |
| |
|
 |
 |
|
|
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
 |