| 1. |
Bereken met de productregel de
afgeleide van de volgende functies: |
| |
|
|
|
|
|
a. |
f(x) = x • √(x + 1) |
e. |
f(x) = x2 • (√x
- x + 6) |
|
b. |
f(x) = (x6
- 2x)
• (4x3 - 8x2) |
f. |
y = (x3 + 4x)
• 1/(x - 1) |
|
c. |
y = (x + 1)3 • x2 |
g. |
y = (2x - 3)4
• (1 - x) |
|
d. |
y = (x + 3x2 ) •
√x |
h. |
y = √(1 - x) • (x3
- x) |
|
|
|
|
|
| 2. |
De vragen b) en d) en e)
hierboven kun je ook vrij eenvoudig zonder de productregel uitrekenen.
Doe dat en controleer of de antwoorden met en zonder de
productregel gelijk zijn. |
|
|
|
|
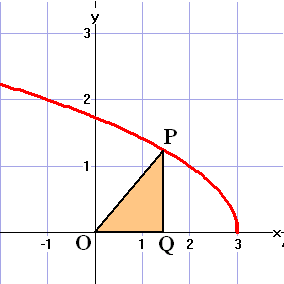
| 3. |
Gegeven is de functie
f(x) = √(3
- x)
Op de grafiek van f ligt punt P met xP
= p en p > 0
|
|
|
|
|
| |
|
|
|
a. |
Druk de lengte van OP uit in p. |
| |
|
|
| |
b. |
Bereken voor welke p de afstand OP minimaal
is. |
|
|
|
|
|
|
|
Q is de projectie van P op de x-as,
dus Q = (p,0) |
|
|
|
| |
|
|
|
c. |
Maak een formule voor de oppervlakte van driehoek
OPQ, en bereken daarna de maximale oppervlakte. |
| |
|
|
|
|
|
|
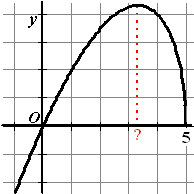
| 4. |
De grafiek van y = x
• √(5 - x) ziet er uit als
hiernaast.
Bereken algebraïsch de x- coördinaat van de top van deze
grafiek. |
|
| |
|
|
|
|
|
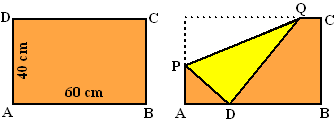
| 5. |
Van een velletje karton
van 40 bij 60 cm wordt de linker bovenpunt omgevouwen tot op de
onderrand AB. Zie de figuur hiernaast. Stel AP = x
Voor de oppervlakte van driehoek APD die daardoor ontstaat geldt
dan:
|
 |
| |
|
|
|
a. |
Toon aan dat deze formule juist is. |
| |
|
|
|
b. |
Bereken algebraïsch de maximale
oppervlakte van driehoek APD. Geef je antwoord in 2
decimalen nauwkeurig. |
| |
|
|
|
| |
|
| 6. |
Een gelijkbenige driehoek heeft omtrek
200, en de lengte van de basis is gelijk aan b
Dan geldt voor de oppervlakte O: O = 5b√(100
- b) |
|
|
|
|
| |
|
|
|
a. |
Toon aan dat deze formule juist is |
| |
|
|
|
b. |
Bereken algebraïsch de maximale
oppervlakte van zo'n driehoek. Geef je antwoord in 2 decimalen
nauwkeurig. |
| |
|
|
|
|
|
|
|
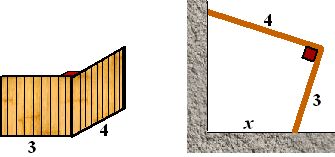
| 7. |
Ik heb twee stukken schutting die
loodrecht aan elkaar vastzitten omdat ze tegen een balk zijn
gespijkerd. de lengtes zijn 3 meter en 4 meter.
Daarmee ga ik een stuk van mijn tuin afzetten zodat mijn kleine
dochtertje daarin kan rondkruipen. Ik zet het stuk schutting in
een hoek van het terras dat door twee loodrechte muren wordt
begrensd. Hieronder staat een bovenaanzicht. |
|
|
|
|
|
|
|
|
|
|
|
Kies de afstand x als in de
figuur hierboven, en verwaarloos de dikte van de balk waartegen
de schotten zijn vastgemaakt.
Voor de afgezette oppervlakte O geldt dan O(x) = 6
+ ½x• √(25 - x2) |
|
|
|
|
|
a. |
Toon aan dat deze formule juist is. |
| |
|
|
|
b. |
Bereken algebraïsch de maximale
oppervlakte. |
| |
|
|
|
|
|
|
|
| 8. |
examenvraagstuk |
|
|
|
|
| |
|
|
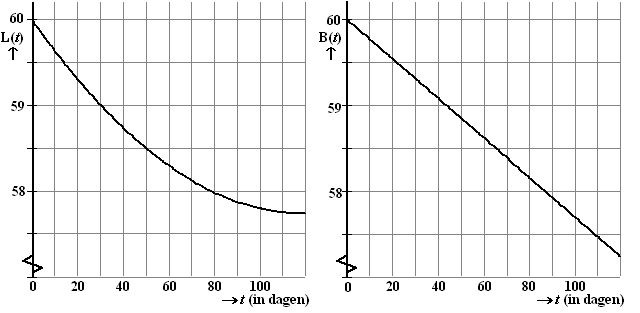
Vers gezaagde planken krimpen in de
eerste maanden nadat ze zijn gezaagd. Door de celstructuur van
het hout vertoont het krimpproces in de lengte een ander beeld
dan het krimpproces in de breedte. In onderstaande grafieken is
te zien hoe de lengte en de breedte van een plank van 60 cm bij
60 cm in de loop van de tijd veranderen. De grafiek rechts is
een rechte lijn. Na t dagen is de lengte gelijk aan L(t)
en de breedte gelijk aan B(t). |
|
|
|
|
|
|
|
|
|
|
|
a. |
Gedurende welke periode krimpt de
plank in de lengterichting sneller dan in de breedterichting? |
| |
|
|
|
b. |
Op t = 0 is de plank vierkant
van vorm. Op welk tijdstip is dat weer zo? |
|
|
|
|
|
Op t = 90 zijn de afmetingen
van de plank: 57,93 in de lengte richting en 57,88 in de
breedterichting. De plank krimpt dan in de lengterichting met
0,0092 cm/dag, en in de breedterichting met 0,023 cm/dag.
O(t) is de oppervlakte in cm2 van de
plank op tijdstip t. |
|
|
|
|
|
c. |
Bereken O'(t) op t = 90
in 1 decimaal nauwkeurig. |
|
|
|
|
|
Mogelijke formules zijn B(t)
= 60 - 0,023t en L(t) = 0,00016t2
- 0,038t + 60 |
|
|
|
|
|
d. |
Op welk tijdstip vermindert de
oppervlakte met een snelheid van 2 cm2/dag? |
|
|
|
|
|
|
|
|
| |
|
 |
 |