|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Meestal gingen we dan in die
noemer kwadraat afsplitsen, en afhankelijk van wat er dan overbleef werd
het een arctanx, of een lnx of je kon breuksplitsen. Maar hoe is het als die vorm in de noemer ook weer tot een macht genomen wordt? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Het blijkt dat ook nu kwadraat
afsplitsen een goed begin is. Alleen is de vorm die daarna overblijft
ietsje lastiger.... Genoeg abstract gelul, tijd voor een voorbeeld: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Kwadraat afsplitsen geeft:
x2 - 6x + 11 = x2
- 6x + 9 - 9 + 11 = (x - 3)2
+ 2 Gebruik nu de substitutie u = x - 3, dus x = u + 3 en dx = du |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Die eerste integraal is (hoop ik)
intussen een makkie. Die u in de teller is (ongeveer) de
afgeleide van u2 + 2 in de noemer, dus dat gaat
iets als (u2 + 2)-2 opleveren als
primitieve (met nog zo hier en daar wat constanten). Maar die tweede integraal dat is een echt probleem....... Bij de wortelvorm √(1 + x2 ) in deze les werkte de substitutie u = tanα. Want dan werd (1 + x2) gelijk aan tan2α. Dat kun je hier ook proberen. u2 + 2 = 2(1/2u2 + 1) = 2( (u√1/2)2 + 1) dus als je ervoor zorgt dat u√1/2 = tanα dan gaat het lukken. Dus neem de substitutie: u = √2 tanα met du = √2/(cos2a) dα |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Maar omdat tan2α + 1 = 1/cos2α = (cosα)-2 gaat dat over in: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Die cos4α
kunnen we primitiveren. Dat staat in
deze les over machten
van sin en cos. De truc was om te gebruiken dat cos2α
= 1/2(1
+ cos2α), dus in dit geval geeft dat: cos4α = (cos2α )2 = (1/2(1 + cos2α))2 = 1/4(1 + 2cos2α + cos22α) = 1/4 + 1/2cos2α + 1/41/2(1 + cos4α) = 1/4 + 1/2cos2α + 1/8 + 1/8cos4α = 3/8 + 1/2cos2α + 1/8cos4α De primitieve daarvan is 3/8α + 1/4sin2α + 1/32sin4α. Omdat we terug moeten naar x maken we eerst van die 2α en 4α weer gewoon α. Dat gaat met de formules sin2α = 2sinαcosα en cos2α = 2cos2α - 1. 1/4sin2α = 1/4 2sinαcosα = 1/2sinαcosα 1/32sin4α = 1/32 2sin2αcos2α = 1/16 2sinαcosα (2cos2α -1) = 1/4sinαcos3α - 1/8sinαcosα Samen geeft dat: 3/8α + 1/4sin2α + 1/32sin4α = 3/8α + 3/8sinαcosα + 1/4sinαcos3α |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
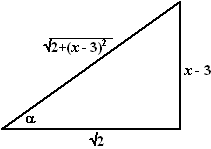
| Om terug naar x-en te
komen kun je de driehoek hiernaast gebruiken. Bedenk dat u = √2 tanα en x = u + 3. De schuine zijde van de driehoek is uiteraard met Pythagoras gevonden. Met deze driehoek kun je nu sinα en cosα uitdrukken in x. Verder geldt, dat als tanα = (x - 3)/√2 dat α = arctan( (x - 3)/√2 ) Daarmee is de primitieve van cos4α gevonden, en uit te drukken in x-en: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| In totaal wordt de primitieve van de oorspronkelijke opgave dan gelijk aan: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Mooi hé? Daar kan ik nou echt van genieten...... Laten we niet de rode draad van deze afleiding uit het oog verliezen: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tot slot nog maar een uitgebreid voorbeeld. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| kwadraat afsplitsen: x2 - 4x + 2 = (x - 2)2 - 2 dus substitueer u = x - 2 dus x = u + 2 en dx = du. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| De eerste integraal
gaat eenvoudig met de kettingregel en is F = -1/2(u2
- 2) De tweede is het probleem. Omdat er nu staat u2 - 2 gebruiken we de substitutie u = √2/cosα en dan is du = √2sinα/cos2α. Het tweede deel wordt dan: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
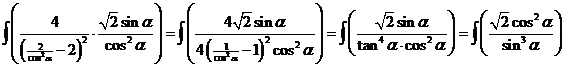 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ga van die cosinussen in de teller ook sinussen maken, dan kun je de integraal splitsen: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
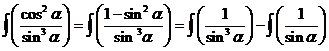 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
In een eerdere les
hebben we al geleerd hoe je primitieven van 1/cosnx
kunt vinden. Daarom maken we hier eerst maar even cosinussen van door te substitueren: α = 1/2π - β, dus dα = -dβ: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
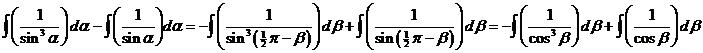 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Uit de genoemde eerdere les komt voor de primitieve van 1/cosnx het volgende resultaat: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| voor n = 3 geeft dat: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Die laatste integraal is makkelijk:
De primitieve van 1/cosx is gelijk
aan F2(x) = ln(1/cosx +
tanx) Dat geeft samen: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| terug naar β = 1/2π - α geeft dan | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Terug naar u
= √2/cosα
geeft cosα
= √2/u en sinα
= √(u² - 2)/u en tanα
= √((u² - 2)/2) (teken maar
weer zo'n driehoekje) Laten we meteen die eerste primitieve van helemaal aan het begin eraan toevoegen, en vergeet ook die factor √2 die we ergens weggelaten hebben niet, dan hebben we: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
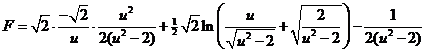 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
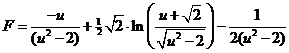 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| vervang tenslotte elke u door x - 2 en je bent er | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
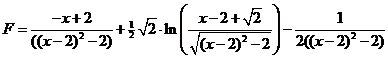 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .....MAKKIE! | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||