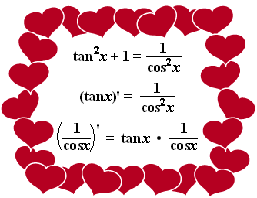machten van tangens en cosinus


Machten van tanx	© h.hofstede (h.hofstede@hogeland.nl)

Altijd als je primitieven met tanx zoekt moet je meteen op jacht gaan naar cosx!!!!
Dat komt omdat tanx en cosx twee dikke vriendjes zijn. Ze zijn direct en via de afgeleiden heel sterk met elkaar verbonden, Als je de één tegenkomt, kom je de ander ook tegen, zoals je in de volgende drie formules wel ziet:

Dat betekent dat je bij het primitiveren combinaties van tanx en cosx handig in elkaar om kunt zetten.

• Met de bovenste formule kun je even machten van tanx en cosx in elkaar omzetten.
• Met de tweede en derde formule kun je de afgeleides proberen zó te krijgen, dat je de kettingregel kunt gebruiken.

De primitieve van:

Als je bijvoorbeeld wilt gebruiken u = tanx, dan zie je aan de tweede formule van de drie hierboven dat je daarvoor twee cosxin de noemer apart moet zetten. Alle andere cos²x die dan nog overblijven kun je met de eerste formule in 1 + tan²x veranderen. Het totaal aantal factoren cosx moet daarvoor dus wel even zijn.

u = tanx als de macht van cosx even is.

Voorbeeld.

De primitieve is daarom F(x) = ¹/₈tan⁸x + ¹/₆tan⁶x + c

En andersom kan het natuurlijk ook: als je wilt gebruiken dat u = ¹/_cosx dan zie je aan de derde formule bovenaan dat je één tanx uit de teller en één cosx uit de noemer apart moet zetten. Dan kun je al die tanx die overblijven omzetten in cosx. Omdat dat per twee gaat (eerste formule) moeten er oorspronkelijk dus een oneven aantal factoren tanx aanwezig zijn (zodat na dat apart zetten er een even aantal overblijft).

u = ¹/_cosx als de macht van tanx oneven is.

Voorbeeld.

Het zelfde voorbeeld als je hiervoor al hebt gezien. Het kan ook zó:

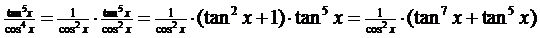Daar staat dus u' • (u⁷ - 2u⁵ + u³ )

De eerste manier was wel eenvoudiger, vond je niet? Als je kunt kiezen dan, zoals hier, zou ik de term met de laagste macht gaan veranderen.

Overigens kan deze primitieve ook gevonden worden door er allemaal sinussen en cosinussen van te maken en dan de kettingregel te gebruiken, kijk maar:

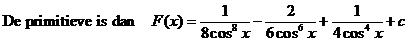Daar staat nu sinx • (cos^-9x - 2cos^-7x + cos^-5x)
Neem u = cosx dan is die sinx de afgeleide daarvan (op een minteken na).

Als de macht van tanx even is en de macht van cosx oneven.

Dat is het laatste overblijvende geval. Maar wel een moeilijke.
De oplossing is: zet al die tan²x van de teller om in ¹/_cos2_x - 1 dan heb je een integraal over met alleen nog maar machten van ¹/_cos_x, kijk maar naar dit voorbeeld:

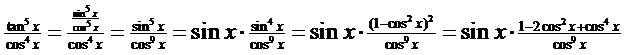Nu zijn alleen nog maar machten van ¹/_cosx over, en hoe je die moet primitiveren staat verderop in deze les.

Alleen machten van tanx (dus m = 0).

Daarvoor herhalen we eerst even wat de primitieve van tanx ook alweer was. Dat is in de les over de kettingregel al behandeld, en het resultaat daar was:

De primitieve van f(x) = tanx is F(x) = -ln│cosx│+ c

Dat kun je handig gebruiken om de primitieve van andere oneven machten van tanx te vinden. Haal tan²x apart en verander die weer in ¹/_cos2_x. Dat is dan weer de afgeleide van die andere tangensen die er nog staan.
Het werkt zó:

Voorbeeld. Geef de primitieve van tan³x

Dat eerste kan met de kettingregel, en dat tweede staat hierboven.
Dus F(x) = ¹/₂tan²x + ln│cosx│ + c

Met hogere oneven machten gaat het precies zo, maar is het wel meer werk, want tan⁵x geeft als antwoord weer een term met tan³x en die moet je dan wéér gaan veranderen. Elke keer die substitutie hierboven gebruiken verlaagt de macht van tan met twee. Dus uiteindelijk kom je er wel....

En als het om een even macht van tanx gaat?

Dan is het erg makkelijk dat de afgeleide van tanx gelijk is aan tan²x + 1.
Kijk maar wat er gebeurt, als je een tan²x apart zet:

tanⁿx = tan²x • tan^n-2 x = tan^n-2x • (tan²x + 1 - 1) = tan^n-2x • (tan²x + 1) - tan^n-2x
Als je nu gaat primitiveren dan kun je voor dat eerste deel gebruiken u = tanx want dan is die tan²x + 1de afgeleide daarvan.

Nu is de primitieve nog niet gevonden, maar de macht van tangens is wel lager geworden. Dus kun je ditzelfde nóg een keer doen om doe macht nog lager te maken, en dan weer... en dan weer.... Net zolang tot je uitkomt bij de primitieven van tan²x. En dan geeft de laatste stap dat de primitieve daarvan is tanx - x

voorbeeld: geef de primitieve van tan⁶x.

tan⁶x = tan⁴x(tan²x + 1 - 1) = tan⁴x • (tan²x + 1) - tan⁴x
tan⁴x = tan²x(tan²x + 1 - 1) = tan²x(tan²x + 1) - tan²x

van deze laatste is de primitieve gelijk aan ¹/₃tan³x - tanx + x
dus van tan⁶x is de primitieve gelijk aan F(x) = ¹/₅tan⁵x - ¹/₃tan³x + tanx - x + c

Alleen machten van 1/cosx (dus n = 0)

Ga van die cosⁿx een cos²x in de teller zetten, dan blijft in de noemer nog cos^{n - 2} x over.
Die teller kun je dan veranderen in 1 - sin²x, en vervolgens kun je de boel splitsen:

Dat laatste stuk aan de rechterkant kun je nu partieel primitiveren:

Daarmee wordt de hele primitieve:

Tenslotte kun je die beide integralen nog samennemen:

Het eindresultaat is dus:

Daarmee is een nieuwe integraal gekregen met een lagere macht. En daar passen we uiteraard weer dezelfde truc op toe. Zo worden de machten met sprongen van twee steeds lager en lager tot we eindigen bij ¹/_cosx of ¹/_cos2_x

De primitieve van ¹/_cos2_x is een oude bekende: F(x) = tanx
De primitieve van ¹/_cosx is gelijk aan F(x) = ln(¹/_cosx + tanx)

Die laatste is geen oude bekende, en ook geen eenvoudige. Als je uit gezonde wiskundehonger gewoon wilt weten hoe het zit, kun je twee dingen doen. Je kunt het bewijs hiernaast doornemen (zeer bevredigend natuurlijk) . Of je kunt de primitieve differentiëren en controleren dat er inderdaad ¹/_cosx uitkomt (minder bevredigend maar beter dan niets doen).

Zo, daar mee kun je dus nu alle ¹/_cosn_x primitiveren.
En het goede nieuws is natuurlijk: je kunt nu ook alle ¹/_sinn_x primitiveren, namelijk door eenvoudig te schrijven
sinx = cos(¹/₂π - x) en dan te nemen u = ¹/₂π - x

Voorbeeld: Geef de primitieve van ¹/_cos5_x

Voorbeeld: Geef de primitieve van ¹/_cos4_x

Tijd voor een samenvatting over cosx en tanx

Het zal je intussen wel duizelen met al die regeltjes, daarom vóór de opgaven nog even alles op een rijtje.

1.	Primitiveer de volgende functies:

	a.	f(x) = tan⁸x	e.

	b.	f(x) = ¹/_cos3_x	f.

	c.	f(x) = ¹/_cos6_x	g.

	d.		h.


© h.hofstede (h.hofstede@hogeland.nl)