| |
 |
|
Machten van sinx en cosx. |
ฉ
h.hofstede (h.hofstede@hogeland.nl) |
|
| |
|
|
|
| Eerst maar even de makkelijkste,
die we zelfs al in een eerdere les hebben gehad.
1. sinnx
of cosnx met n een oneven
getal. |
| |
|
|
|
Dat gaat (bijvoorbeeld bij sinnx)
als volgt:
Zet ้้n van die sinx eventjes apart. Dan hou je een even
macht over.
Maar elke sin2x in het overgebleven deel kun
je met de formule sin2x = 1 - cos2x
veranderen in een cos2x
Wat over is kun je primitiveren (stel cosx = u
dan is de afgeleide ongeveer die ene sinx die je apart had gezet)
Voorbeeld. Primitiveer f(x)
= sin5x.
sin7x = sinx sin6x =
sinx (sin2x)3 =
sinx (1 - cos2x)3 = sinx
(1 - 3cos2x + 3cos4x - cos6x).
(bij dat haakjes wegwerken was trouwens het binomium van
Newton wel erg makkelijk, vond je niet?).
Noem nu cosx = u dan is die sinx de afgeleide
daarvan (op een minteken na).
De primitieve is dan F(x) = -cosx +
1/4cos3x
- 3/5cos5x
- 1/7cos7x
+ c. |
| |
|
|
|
|
2. Een mengsel van sinnx
cosmx met minstens ้้n oneven macht. |
| |
|
|
|
Nou, dat gaat natuurlijk precies
hetzelfde. Kies degene met de oneven macht (als beide machten oneven
zijn zou ik de kleinste nemen. Als je graag veel wiskundewerk verricht
neem je natuurlijk de grootste). Pas op die oneven macht bovenstaande
methode toe.
Voorbeeld. Primitiveer cos3x
sin4 x
cos3x sin4x = cosx
cos2x sin4x = cosx
(1 - sin2x) sin4x = cosx
(sin4x - sin6x).
Noem nu sinx = u dan is die cosx daar de
afgeleide van.
De primitieve is dan F(x) =
1/5sin5x
- 1/7sin7x
+ c. |
| |
|
|
|
|
3. Als beide
machten even zijn. |
| |
|
|
|
| Dan is er helaas niet ้้n kant en
klaar recept om ze allemaal op te lossen. Soms is het lastig om een
oplossing te vinden, soms zijn er meteen meerdere mogelijke oplossingen.
Formules die daarbij wel vaak erg handig zijn, zijn de volgende drie, je
herkent ze vast als de verdubbelingsformules: |
| |
|
cos2x =
1/2
+ 1/2cos2x
sin2x = 1/2
- 1/2cos2x
sinx cosx = 1/2sin2x
|
|
| |
't Is eigenlijk steeds een beetje
prutsen met deze drie vergelijkingen en daarmee de machten van sinx
en cosx kleiner maken.
Voorbeeld op twee manieren. Primitiveer
f(x) = sin2x cos2x
eerste manier.
vervang cos2x en sin2x
direct met de bovenstaande formules.
Dat geeft sin2x cos2x=
(1/2
+ 1/2cos2x)(1/2
- 1/2cos2x)
= 1/4
- 1/4cos22x
En nou kun je die laatste cos22x weer vervangen,
door 1/2
+ 1/2cos4x
Dat geeft f(x) = 1/4
- 1/4(1/2
+ 1/2cos4x)
= 1/4
- 1/8
- 1/8cos4x
= 1/8
- 1/8cos4x
De primitieve is dan F(x) = 1/8x
- 1/32sin4x
+ c
tweede manier.
sin2x cos2x = (sinx cosx)2
en dat tussen die haakjes kun je vervangen door 1/2sin2x.
Dat geeft f(x) = 1/4sin22x
. Nu kun je die sin22x weer vervangen door
1/2
- 1/2cos4x.
Dat geeft f(x) = 1/4(1/2
- 1/2cos4x)
= 1/8
- 1/8cos4x
en uiteraard dezelfde primitieve als hierboven.
Nou ja... uiterแแrd....
Het hoeft niet zo te zijn dat er met verschillende methodes precies
dezelfde primitieve uitkomt. Het zou kunnen dat die c anders is.
De primitieven die je krijgt moeten natuurlijk wel op een constante na
hetzelfde zijn. |
| |
| |
|
|
|
|
|
|
| 1. |
Bereken primitieven van de volgende functies: |
| |
|
|
|
|
|
|
| |
a. |
f(x) = cos6x |
|
d. |
f(x) = cos5x
sin5x |
|
| |
|
|
|
|
|
|
| |
b. |
f(x) = sin3x |
|
e. |
f(x) = cos4x
sin2x |
|
| |
|
|
|
|
|
|
| |
c. |
f(x) = cos4x
sin3x |
|
f. |
f(x) = sin4x |
|
| |
|
|
|
|
|
|
|
|
4. Je kunt het soms ook
gebruiken bij breuken! |
| |
|
|
|
Dat trucje van ้้n zo'n oneven
sinx of cosx even apart zetten, dat werkt natuurlijk ook
bij sommige breuken.
Kijk maar: |
| |
|
|
|
| Voorbeeld. |
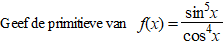 |
|
|
| Haal daarboven ้้n
sinx apart en ga dan die even macht van sinx die
overblijft veranderen in cosx, zoals je intussen waarschijnlijk
al gewend bent. |
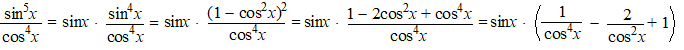 |
Als cosx =
u dan staat daar gewoon de primitieve van u-4
- 2u-2 + 1
Dat is F(x) = 1/3cos-3x
- 2cos-1x - x + c (de mintekens
omdat de afgeleide van cosx gelijk is aan -sinx). |
| |
|
|
|
|
Waarschuwing: Dit werkt
natuurlijk alleen als je een sinx of cosx uit de
teller apart kunt zetten!!!! |
| |
|
|
|
 |
|
ฉ
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|