© h.hofstede (h.hofstede@hogeland.nl)
De lengte van een parameterkromme.

Voorkennis:
afstand als integraal.
één keer doorlopen.
Om de lengte van een parameterkromme te bepalen hoef je slechts twee formules met elkaar te combineren.
Bij het opstellen van integralen hebben we de volgende formule voor de afgelegde weg S en de snelheid v gehad:
 

 
En bij het berekenen van de snelheid van punt P van een parameterkromme vonden we in deze les:

Omdat de lengte van een parameterkromme gelijk is aan de afgelegde weg krijg je als je deze twee formules samenvoegt:
Dat is alles.....

Denk erom dat de twee grenzen van de integraal t-waarden zijn!!!!
Het enige waar je op moet letten is, dat je die t-grenzen van de integraal zó kiest dat tussen die twee t's de kromme precies één keer wordt doorlopen. Daarna is het een kwestie van invoeren in je GR en via het CALC-menu de integraal berekenen. Algebraïsch hoef je het niet te kunnen; die primitieve is bijna altijd veel te ingewikkeld.

Ok, ....zucht....ik geef het toe .... We hadden voor deze formule (helaas) natuurkunde nodig. Dat gedoe met snelheid en afgelegde weg en zo, dat was vrij natuurkundig. Als je daar een erge hekel aan hebt, en je liever tot de pure en veel mooiere wiskunde beperkt kun je hiernaast nog een bewijs van die formule voor L vinden. Deze keer echt alleen wiskundig, dat beloof ik je....
 
   
  OPGAVEN
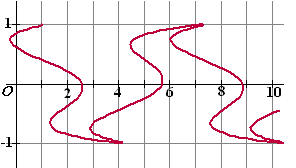
1. De baan van punt P wordt gegeven door:
x(t) = t + cos(4t)  en   y(t) = cost
Hiernaast zie je de vorm van die baan.

     
  a. Bereken algebraïsch de baansnelheid van P in het punt waar t = 1/3π
     
  b. Bereken de maximale snelheid van P.
     
  c. Bereken de afstand die P aflegt tussen t = 0 en t = π.
       
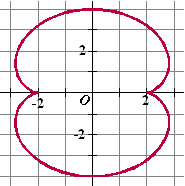
2. Een nephroïde is een soort ingezakte "acht". Hiernaast staat de nephroïde met vergelijkingen:
x(t) = 3cost - cos(3t)  en   y(t) = 3sint - sin(3t)

  a. Bereken met je GR de omtrek van deze nephroïde
     
  Voor de snelheid van punt P geldt:  v(t) = 6 • ‌ sint ‌
       
  b. Toon dat aan.  
     
  c. Bereken met deze laatste formule nogmaals, maar nu algebraïsch, de omtrek van deze nephroïde.
       
3. Een ellips met lange as 4 en korte as 2 heeft parametervoorstelling:  x(t) = 2cos(t) en  y(t) = sin(t)
Bereken in drie decimalen nauwkeurig de omtrek van deze ellips.
   

9,688
     
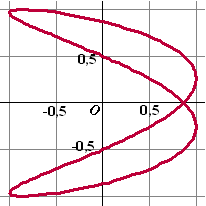
4. De baan van punt P wordt gegeven door:   
x(t) = sin 2t   en   y(t) = sin (t - π/3)
met t in [0, 2π]. Hierin zijn x en y in cm en t in seconden.

Bereken de lengte van de baan van P in twee decimalen nauwkeurig.

     

9,34
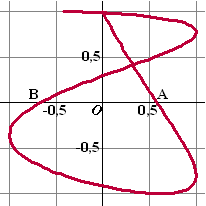
5. De baan van punt P wordt gegeven door: 
x(t) = sin(t2)   en   y(t) = cos2t
met t in [0, π].   Hierin zijn x en y in cm en t in seconden.
De baan snijdt de x-as in de punten A en B.

     
  a. Bereken de snelheid van P in punt B.
   

4,04
  b. Bereken de lengte van de baan tussen A en B.
     

3,73
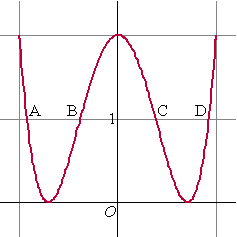
6. De baan van punt P wordt gegeven door:  x(t) = cos t    en   y(t) = 1 + cos 4t
met t in [0, π]. Hierin zijn x en y in cm en t in seconden.
De baan snijdt de lijn y = 1 in de punten A, B, C , D en E.

     
  a. Bereken de snelheid van P in punt A.
     
  b. Bereken de lengte van de baan tussen A en B.
       
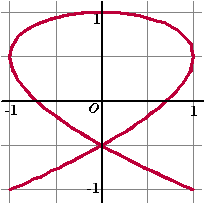
7. De baan van punt P wordt gegeven door de kromme:
x(t) = sin 3t   en   y(t) = cos 2t
met t in [a , b]
Hierin zijn x en y in cm en  t in seconden.
De kromme wordt precies één keer doorlopen.

     
  a. Kies geschikte waarden voor a en b en plot de kromme.
     
  b. Punt P passeert de assen vijf keer. Bereken bij elke doorgang de snelheid van P.
       
  c. Bereken de maximale snelheid van P.
       
  d. Bereken de lengte van de baan van P.  
       
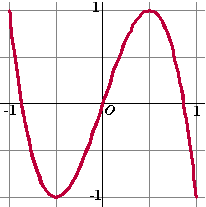
8. Gegeven is parameterkromme K met vergelijkingen:
x(t) = sin t  en  y(t) = sin 3t
Deze kromme voldoet aan de vergelijking  y = 3x - 4x3

     
  a. Bewijs dat dat zo is. Bedenk daarbij dat sin 3t te schrijven is als  sin (t + 2t)
     
  b. Bereken met deze vergelijking de lengte van K
     
  c. De lengte van K is ook te berekenen door een formule op te stellen voor de snelheid van een punt als functie van de tijd t, en daarna deze snelheidsfunctie te integreren. Doe dat.
       
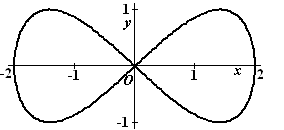
9. Examenvraagstuk VWO Wiskunde B, 2008

Hiernaast is in een assenstelsel de kromme k getekend, gegeven door

 
       
 

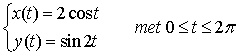Deze kromme is symmetrisch ten opzichte van de x-as en de y-as.

De kromme k heeft vier punten waarin de raaklijn horizontaal loopt. Deze vier punten zijn de hoekpunten van een rechthoek.
       
  a. Bereken de oppervlakte van deze rechthoek.
     

4√2
  b. Er zijn twee punten met positieve x-coördinaat op k waarvan de y-coördinaat gelijk is aan 1/2 . Bereken in één decimaal nauwkeurig hoe ver die twee punten van elkaar liggen.
     

1,4
  c. Bereken in één decimaal nauwkeurig de lengte van de kromme k.
     

12,2
       
© h.hofstede (h.hofstede@hogeland.nl)