hellinggetal bij lineair verband


Het Hellinggetal	© h.hofstede (h.hofstede@hogeland.nl)

We zagen al eerder dat de grafieken van y = a • x altijd rechte lijnen zijn door de oorsprong.

Hiernaast staan in één figuur de grafieken van y = ¹/₃x en y = ¹/₂x
en y = x en y = 2x en y = 3x en y = 4x getekend.

Daaraan is duidelijk te zien dat de grootte van a bepaalt hoe steil de lijn loopt. Hoe groter a, des te steiler loopt de lijn.
Daarom noemen we a vanaf nu het hellinggetal van de lijn.

(een mooier woord ervoor is trouwens richtingscoëfficiënt)

Wat zegt dat getal a nou precies over de grootte van de helling?

Als je de grafieken hierboven goed bestudeert, dan krijg je misschien het vermoeden dat het getal a zegt hoeveel de grafiek stijgt bij één stapje naar rechts.
Controleer het maar, het klopt echt elke keer.

"1 naar rechts, a omhoog"

(De echte liefhebbers kunnen het

nog lezen, natuurlijk).

Wat gebeurt er als a negatief is?

Ik denk dat iemand die zou moeten gokken het vanzelf goed gokt....
Laten we dat testen......
Gok eens wat er zou gebeuren als a negatief is, en controleer daarna hieronder of jouw gok inderdaad goed was.

Als het getal a negatief is, dan:

Ja Dûh;
Dan gaat de lijn bij 1 stapje naar rechts a omlaag in plaats van a omhoog natuurlijk!

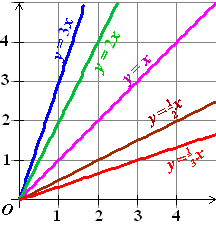
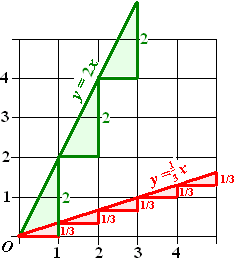
Schets de volgende grafieken in één figuur. Doe dat zonder een tabel te maken of je GR te gebruiken.

y = 5x en y = 2,5x en y = -0,5x en y = -3x

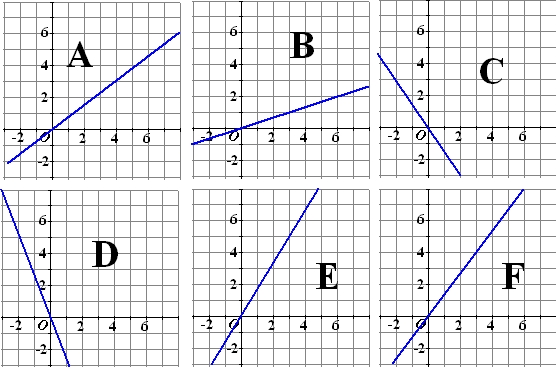
Geef formules bij de onderstaande grafieken.

A: y = 0,75x
B: y = ¹/₃x
C: y = -1,5x
D: y = -2,5x
E: y = 1²/₃x
F: y = 1¹/₃x

Leg uit of de volgende punten op één lijn door de oorsprong liggen:

(2, 7) en (11, 38¹/₂) en (19, 66)

NEE

(3, 4) en (18, 24) en (19¹/₂, 26)

(-3, 5) en (6, -10) en (-9, 15)

Groep 6 van de obesitas-school DDV (De Dikke Vrienden), besluit te gaan afvallen. Op 1 januari laten ze zich door een notaris wegen en beginnen ze een dieet. Zes maanden later, op 1 juli, laten ze zich weer wegen. Ze hebben vooraf buren en familieleden als sponsor gevonden die hen voor elke kilo die ze zijn afgevallen een bepaald bedrag zullen geven. Dat bedrag per kilo noemen we het "sponsorbedrag".
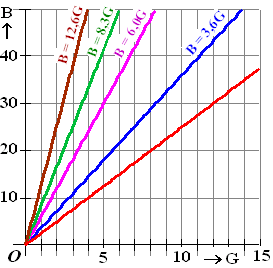
Hieronder staat een grafiek met op de x-as het gewicht (G) dat er af is gegaan en op de y-as het bedrag (B) dat iemand krijgt. Elke lijn hoort bij een verschillend sponsorbedrag.

Welke formule hoort er bij de onderste rode grafiek?

B = 2,5G

Janneke is een beetje een apart geval. Ze heeft met haar sponsoren een bedrag van 6 euro per kilo afgesproken, maar een aantal sponsoren hebben daar een bovengrens van 5 kilo aan gesteld. Die willen dus maximaal 30 euro betalen. Van de rest van haar sponsoren krijgt ze voor elke kilo boven de 5 nog maar 3,60 euro per kilo.

Geef in bovenstaande grafiek aan hoe het bedrag van Janneke als functie van het aantal afgevallen kilos zal verlopen.

Gerard is niet zo slim geweest; hij krijgt van zijn sponsoren voor elke afgevallen kilo 5 euro, maar hij heeft met zijn sponsoren afgesproken dat hij, als hij zwaarder zal worden, hij hen per kilo 10 euro zal betalen!!!
Teken de grafiek van Gerard, zowel het deel waar hij winst maakt, als het deel waar hij geld zal moeten betalen.

Ons belastingstelsel is progressief. Dat betekent dat iemand die meer verdient niet alleen meer belasting betaalt, maar ook een hoger percentage belasting. De volgende tabel geldt voor mensen tot 65 jaar.
Let op: de percentages uit de tabel worden alleen betaald over het extra bedrag, gerekend vanaf de vorige kolom.
Bijvoorbeeld: iemand die 25000 verdient betaalt over de eerste 17046 euro 34,15% belasting en over de resterende 7954 euro nog 41,45%

Het gedeelte van het inkomen:	tm €17046	17047 tm 30631	30632 tm 52228	52229 en meer
Belasting over dat gedeelte:	34,15%	41,45%	42,00%	52,00%

Maak een grafiek voor het totale bedrag (dus niet het rentepercentage!) aan belasting dat iemand moet betalen als functie van zijn inkomen.

Een roltrap is 12 meter lang.
Drie jongens, Klaas, Peter en Guus, stappen gelijktijdig de trap op.
Klaas gaat met de trap naar boven en meet zijn afstand A (in m) tot het beginpunt van de trap als functie van de tijd t in seconden met t = 0 het moment dat hij op de trap stapt.

Geef een formule voor K(t) en schets de grafiek van K(t) als Klaas na 20 seconden boven is.

Peter is wat ongeduldiger en loopt op de trap zelf ook nog naar boven. Daardoor is hij 10 seconden eerder dan Klaas boven. Zijn afstand wordt gegeven door P(t)

Geef een formule voor P(t) en schets de grafiek van P(t) in dezelfde figuur als die van K(t)

Voor Guus geldt de formule G(t) = 1,5t.
Leg duidelijk uit wat het getal 1,5 in deze formule zegt over het gedrag van Guus.

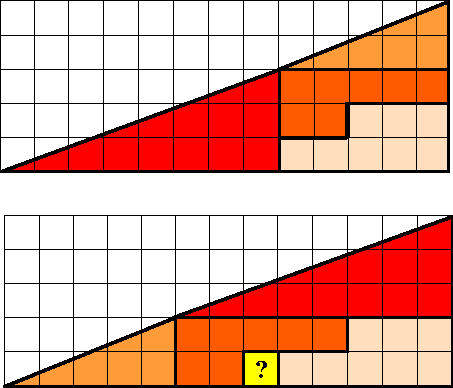
In de driehoeken hieronder zijn 4 dezelfde figuren op een verschillende manier gerangschikt. Echter de bovenste driehoek heeft oppervlakte 32,5 en de onderste slechts 31,5 want daar zit een geel gat in.
Hoe kan dat?

Onderzoek met hellinggetallen of de schuine zijde van de driehoek wel een echte schuine zijde is. Leg daarna uit wat er fout is aan de figuur en waar het ene vakje verschil vandaan komt.

In het artikel "Carbon Emissions Linked To Global Warming In Simple Linear Relationship" beschrijft de wetenschapper Damon Matthews (Concordia University) een recht evenredig verband tussen de CO₂-emissies en de opwarming van de aarde.
Uit een vergelijking van klimaatmodellen onderling in combinatie met historische temperatuurgegevens maakte hij het volgende model: T (°C) = 0,0000000000015 × CO₂ (ton)

Een vliegtuigvlucht kost 6 ton CO₂. Bereken voor hoeveel opwarming zo'n vlucht zorgt, en hoeveel zulke vluchten nodig zijn om een opwarming van één graad te geven.

1,1• 10¹¹

De huidige uitstoot van CO₂ bedraagt zo'n 4 ton CO₂ per aardbewoner per jaar.
De jaarlijkse opwarming daarbij is 0,04 ºC per jaar.

Bereken uit deze gegevens hoeveel bewoners er ongeveer op aarde zijn.

6,7 miljard

Examenvraagstuk HAVO wiskunde A, 2007.

Voor bergbeklimmers is het belangrijk te weten op welke hoogte ze zich bevinden. Daarvoor gebruiken ze tegenwoordig hoogtemeters die de hoogte met behulp van de luchtdruk meten. Immers, hoe hoger je komt, hoe lager de luchtdruk.

Toen Francisco José de Caldas in 1791 het Andesgebergte overstak, was er geen hoogtemeter. Hij bedacht er zelf een: hij kookte water in een pannetje en mat de temperatuur op het moment dat het water begon te borrelen en kwam op die manier de hoogte te weten.

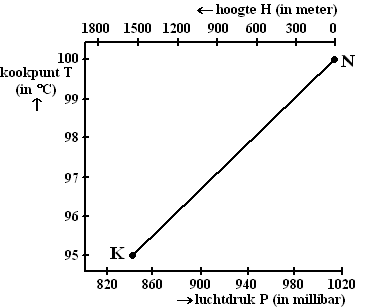
Op zeeniveau (op 0 meter hoogte) is de luchtdruk 1013 millibar en kookt water bij 100 °C. Kom je hoger, dan daalt de luchtdruk, maar gaat ook het kookpunt (de temperatuur waarbij water begint te borrelen) van water omlaag. Zo kookt water op de top van de Mount Everest (8850 meter) al rond de 70 °C. Het kookpunt van water is dus een maat voor de hoogte. In de figuur hieronder zie je hoe de hoogte H, de luchtdruk P en het kookpunt T met elkaar samenhangen. De drie schaalverdelingen zijn lineair.

In deze figuur is punt K getekend: bij een hoogte van 1530 meter is de luchtdruk 845 millibar en het kookpunt 95 °C. Ook punt N is getekend (H = 0 meter, P = 1013 millibar en T = 100 °C).

Thijs is op vakantie in de Duitse Eiffel. Hij wil met de methode van De Caldas weten op welke hoogte hij zit. Hij kookt water en meet de temperatuur. Het water kookt bij 98,1 °C.

Op welke hoogte zit Thijs? Geef in de figuur aan hoe je aan je antwoord bent gekomen.

Tot 2 km hoogte gebruiken bergbeklimmers verschillende vuistregels. Een vuistregel voor het verband tussen hoogte en luchtdruk is: "bij elke stijging van 100 meter neemt de luchtdruk met 11 millibar af"

Onderzoek of deze vuistregel in overeenstemming is met de figuur hierboven.

Met behulp van de figuur hierboven kun je ook een vuistregel maken voor het verband tussen de hoogte en het kookpunt. Ook deze begint met: "bij elke stijging van 100 meter …

Geef deze vuistregel. Licht je werkwijze toe.

10.

Kangoeroewedstrijd.

Vijf atleten hebben hardgelopen. In het assenstelsel hiernaast kun je voor elke atleet zijn of haar tijd en afstand aflezen.

Wie liep het hardst?