Vermenigvuldigen.

© h.hofstede (h.hofstede@hogeland.nl)
Wat gebeurt er in het complexe vlak als je twee getallen met elkaar vermenigvuldigt?
Dat is niet zomaar eenvoudig te zien (zoals bij optellen wel  het geval was weet je nog: kop-aan-staart).
Hiernaast zie je drie keer z1 •  z2 =  z  waarbij dezelfde kleuren bij elkaar horen.
Er is niet makkelijk een patroon te zien of een regel af te leiden, denk ik.
Zie jij zomaar hoe die z met dat gekleurde rondje erom ontstaat uit die andere twee met dezelfde kleur?

Ik niet.....
In zo'n geval moet je een probleem wetenschappelijk aanpakken. Dat betekent: niet teveel tegelijk veranderen!
etappe 1:  vermenigvuldigen met een reëel getal.

Kijk; hiernaast is het veel makkelijker. Daar is een complex getal z achtereenvolgens met 2, met 3 en met 4 vermenigvuldigd.
Ik denk dat het resultaat daarvan makkelijk te doorgronden is.:
vermenigvuldigen met een reëel getal:
maak de afstand (r) tot de oorsprong zoveel keer zo groot.
 
Het bewijs daarvan is natuurlijk met de poolcoördinaten makkelijk te leveren:
pz = p • (rcosφ + rsinφ) = pr • (cosφ + sinφ) = znieuw    dus rnieuw wordt gelijk aan proud
etappe 2 : neem de afstand tot de oorsprong gelijk aan r = 1.

Hieronder staat drie keer de vermenigvuldiging  z = z1 • z2. Daarbij is de afstand van z1 en z2  tot de oorsprong steeds beiden 1 genomen. 

Je ziet dat z ook steeds weer op de eenheidscirkel ligt (wist je al:  r blijft 1).
Vermenigvuldigen lijkt een soort draaiing op te leveren. De punten blijven op de cirkel liggen.
Als je goed naar de draaihoeken kijkt dan zie je misschien dat de hoek die bij z hoort gelijk is aan de hoeken van z1 en z2 bij elkaar opgeteld.
bij vermenigvuldigen van complexe getallen moet je de hoeken j bij elkaar optellen

etappe 3:  SAMEN.
Oké, zullen  we maar weer "driemaal raden" doen?
We hebben intussen al ontdekt:
• als je vermenigvuldigt met het reële getal r dan wordt de afstand tot de oorsprong r keer zo groot.
• als je vermenigvuldigt met cosφ + isinφ  (een punt op de eenheidscirkel) dan geeft dat een draaiing over hoek φ.
Je moet de hoek φ optellen bij de hoek van het getal dat je al had.
Als je beiden doet, dan hoef je dus niet driemaal te raden, maar je kunt meteen eigenlijk wel zeggen wat er gebeurt.
Dan gebeuren namelijk beide bovenstaande effecten.
Dat levert wat we noemen een Draaivermenigvuldiging op:
Vermenigvuldig  z1 = r1(cosφ1+ isinφ1)  met  z2 = r2(cosφ2 + isinφ2)
Dat geeft z1 • z2  =  r1r2 • (cos(φ1 + φ2) + isin(φ1 + φ2))

Ofwel:  Tel de hoeken op, en vermenigvuldig de afstanden.
Ofwel:  | z1 • z2 | = | z1 | • | z2 |  en   arg(z1 • z2) = arg(z1) + arg(z2)

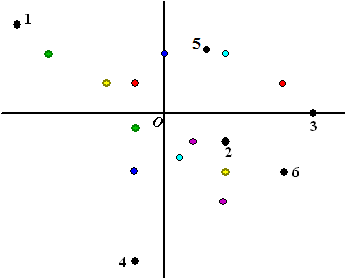
1. Hieronder zie je een complex vlak met allerlei gekleurde punten. De punten met dezelfde kleur worden met elkaar vermenigvuldigd en leveren dan als resultaat één van de genummerde zwarte punten op.
Leg uit welk nummer bij welke kleur hoort.

 
2. Bereken van de volgende complexe getallen  r en een mogelijke φ. Doe dat zonder de vermenigvuldigingen werkelijk uit te voeren.
a. (3 + 3i) • (2 + 2i)
12 en  90°
c. i • (-6√3 - 6i)
15,5 en  -122°
b. (4 - i)2
14 en  -28°
d. (1 - i) • (3 + 4i)
5Ö2 en  8°
3. a. Leg uit hoe ook uit deze regel volgt dat draaien over 90º hetzelfde is als vermenigvuldigen met i.
     
b. Waarmee zou je moeten vermenigvuldigen als je wilt draaien over 30º?
             
1/2√3+1/2i
   

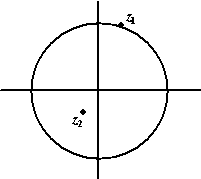4. Hiernaast staan in het complexe vlak twee getallen z1  en z2 getekend, en een cirkel waar z1 op ligt
Het punt  z = z1 · z2 blijkt ook op de cirkel te liggen.
         
  a. Teken de plaats van z
         
  b. Teken de plaats van het getal i.
5. Probeer eens te raden hoe het  delen  van twee complexe getallen in zijn werk gaat in het complexe vlak.
Bedenk dat delen natuurlijk het omgekeerde is van vermenigvuldigen.
Controleer daarna met een paar voorbeelden of jouw ideeën inderdaad kloppen.
               
6. Hiernaast zie je in het complexe vlak een getal z aangegeven dat op afstand 9 van de oorsprong ligt.
 

Teken in deze figuur ook de plaats van  z - i√z

Doe dat zonder berekeningen met complexe getallen te maken.
Geef een duidelijke uitleg.

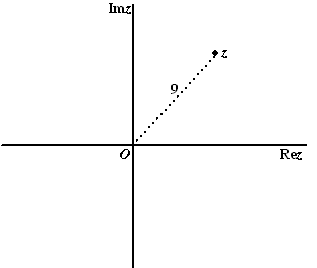Een beroemde formule.

Als je uitrekent  (2 + i)(3 + i)  dan geeft dat, als je het goed doet,  5 + 5i
Maar als je de argumenten van deze drie complexe getallen bekijkt, dan geeft dat:  
arctan(1/2) + arctan(1/3) = arctan(1) = π/4
Kijk! dat is toch handig! Zo kun je met complexe getallen allerlei formules voor arctanx aantonen.

Probeer nu zelf eerst deze volgende beroemde formule aan te tonen:
 

4 • arctan(1/5)  - arctan(1/239) =  π/4
 
Deze formule is later, zoals we nog zullen zien, erg handig gebleken om π te benaderen.
 
Machtsverheffen.
Als je je maar bedenkt dat machtsverheffen niets anders is dan herhaald vermenigvuldigen, dan is dit een makkie.
Als je bijvoorbeeld wilt uitrekenen  (1 + i)6  dan is dat   (1 + i)(1 + i)(1 + i)(1 + i)(1 + i)(1 + i)
Maar 1 + i = √2 • (cos45º + isin45º)

Dus 
(i + i) • (1 + i) = √2 • √2 (cos90º + isin90º)
(i + i) • (1 + i) • (1 + i) = √2 • √2 • √2 • (cos135º + isin135º)
.....
(1 + i)6 =  (√2)6 • (cos (6 • 45º) + isin(6 • 45º))

als   z = r • (cosφ + isinφ)  dan is   zn =  rn • (cosnφ + isinnφ)
   

   

poolcoördinaten

    

vectoren
7. Geef de volgende getallen in de vorm a + bi.  Doe dat zonder de complexe getallen van je rekenmachine te gebruiken.
             
a. (3 + i)4

28+96i
d. (1 - i)5

-4+4i
b. (-1 - 0,3i)100

-47,9 + 56,9i
e. (2 + 2i)3

-16+16i
  c. (1/2 - 1/2iÖ3)10

-0,5+0,5iÖ3
f. (√2 + i√2)6

-64i
               
8. Als je het getal 1 + i gaat machtsverheffen, dus (1 + i)n gaat bepalen voor allerlei n, dan kom je regelmatig uit op een getal dat op de imaginaire as ligt. 
We beginnen met n = 0 en laten n daarna met stapjes van 1 toenemen. We bekijken alle getallen op de imaginaire as.
Wat is op die manier het vijfde getal dat op de imaginaire as ligt?
           

512i
               
9. a. Als je neemt r = 1  en  n = 2 dan kun je met draaivermenigvuldigingen  formules voor  cos2x en sin2x afleiden.
Doe dat.
               
  b. Leid formules af voor cos3x en sin3x
               
  c. Toon aan dat  cos(α + β) = cosαcosβ - sinαsinβ  en dat  sin(α + β) = sinαcosβ + cosαsinβ
               
10. Voor een complex getal z op de eenheidscirkel geldt dat  1/z  gelijk is aan de geconjugeerde van z.
               
  a. Toon dat aan.
               
  b. Laat zien dat daaruit volgt dat  cos2φ + sin2φ = 1
 
 

© h.hofstede (h.hofstede@hogeland.nl)