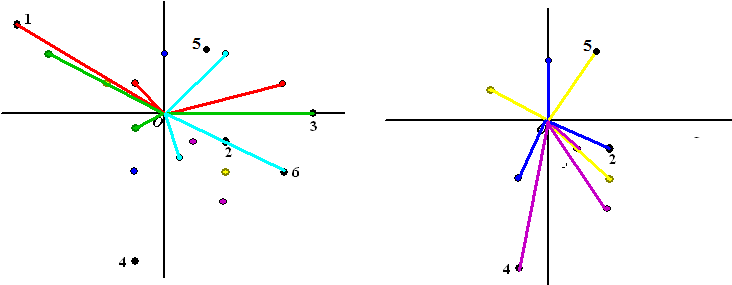
|
|||||
| 1. | |||||
|
|
|||||
| 2. | a | (3 + 3i)
heeft r = 3√2 en
φ = 45º
(2 + 2i) heeft r = 2√2 en φ = 45º Samen geeft dat r = 12 en φ = 90º |
|||
| b. | 4 - i
heeft r = √17 en
φ = tan-1 (-1/4)
= -14º in het kwadraat geeft dat r = 17 en φ = -28º |
||||
| c. | i
heeft r = 1 en
φ = 90º -6Ö3 - 6i heeft r = √(144) = 12 en φ = 210º samen geeft dat r = 12 en φ = 300º |
||||
| d. | (1 - i)
heeft r = √2 en
φ = -45º (3 + 4i) geeft r = 5 en φ = tan-1 (4/3) = 53,1º samen geeft dat r = 5√2 en φ = 8,1º |
||||
| 3. | a. | i heeft r
= 1 en
φ = 90º Dat r = 1 doet niets met de afstand, dus er wordt allen gedraaid over 90º |
|||
| b. | Dan moet je
vermenigvuldigen met het getal waarvoor r = 1 en
φ = 30º Dat is z = cos30º + i sin30º = 1/2√3 + 1/2i |
||||
| 4. | a. | Dan kom je midden tussen beide
punten (wat de hoeken betreft) op de cirkel uit. zie hiernaast. |
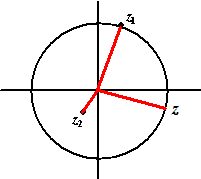 |
||
| b. | Als z1
· z2 op de cirkel
ligt, dan heeft het vermenigvuldigen met z2 de afstand
niet veranderd, dus ligt z2 op de eenheidscirkel. Dat geeft de plaats van i |
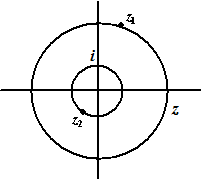 |
|||
| 5. | Als je uitrekent z1/z2 Dan moet je doen φ1 - φ2 en r1/r2 Controleer dat zelf maar...... |
||||
| 6. | √z heeft straal 3 en hoek de
helft van die van z (rood) i√z vind je door √z over 90º te draaien (blauw) -i√z is de andere kant op (groen) Tel die groene vector bij z op (kop aan staart) , en je komt uit bij z- i√z |
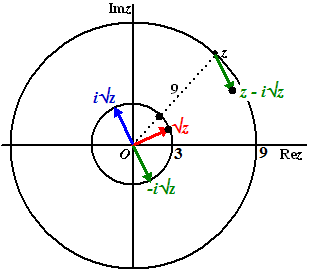 |
|||
| 7. | a. | 3 + i
heeft r = √10 en
φ = tan-1(1/3)
= 18,4º (3 + i)4 heeft dan r = (√10)4 = 100 en φ = 4 · 18,4º = 73,7º Dat is het getal 100 (cos73,7º + isin73,7º) = 28 + 96i |
|||
| b. | -1 - 0,3i
heeft r = √(1,09) en
φ = tan-1 (0,3/1) = 16,7º
maar dan 180º verder, dus 196,7º (-1 - 0,3i)100 heeft r = (√1,09))100 = 74,35 en φ = 100 · 196,7º = 19670º Dat is het getal 74,35 · (cos19670º + isin19670º) = -47,9 - 56,9i |
||||
| c. | 1/2
- 1/2i√3
heeft r = 1 en
φ = -60º (1/2 - 1/2i√3)10 heeft dan r = 110 = 1 en φ = 10 • -60 = -600º Dat is het getal cos(-600º) + isin(-600º)) = -0,5 + 0,5i√3 |
||||
| d. | 1 - i heeft
r = √2 en
φ = tan-1(-1) = -45º (1 - i)5 heeft dan r = (√2)5 = 4√2 en φ = 5 • -45º = -225º Dat is het getal 4√2(cos(-225º) + isin(-225º)) = -4 + 4i |
||||
| e. | 2 + 2i
heeft r = √8 en
φ = tan-1(1) = 45º (2 + 2i)3 heeft dan r = (√8)3 = 8√8 en φ = 3 • -45º = -135º Dat is het getal 8√8(cos(-135º) + isin(-135º)) = -16 - 16i |
||||
| f. | √2 + i√2
heeft r = 2 en
φ = tan-1(1) = 45º (√2 + i√2)6 heeft dan r = 26 = 64 en φ = 6 • 45º = 270º Dat is het getal 64(cos(270º) + isin(270º)) = -64i |
||||
| 8. | De hoek van 1 + i
is 45º Dus (1 + i)2 heeft een hoek van 90º en ligt op de imaginaire as. na nog vier keer vermenigvuldigen is er 4 • 45º = 180º bijgekomen, dus ligt het getal weer op de imaginaire as. Dus (1 + i)2 en (1 + i)6 en (1 + i)10 en (1 + i)14 en (1 + i)18 en ...... liggen op de imaginaire as. De vijfde in de rij is (1 + i)18 1 + i heeft r = √2 en φ = 45º (1 + i)18 heeft r = (√2)18 = 512 en φ = 18 • 45º = 810º = 90º Dat is het getal 512i |
||||
| 9. | a. | (cosφ
+ isinφ)2 = cos2φ
+ 2icosφsinφ
- sin2φ = (cos2φ
- sin2φ) + i(2cosφsinφ) (cosφ + sinφ)2 = cos2φ + isin2φ van die getallen moeten het reële deel en het imaginair deel gelijk zijn, dus moet gelden cos2φ = cos2φ - sin2φ en sin2φ = 2sinφcosφ |
|||
| b. | (cosφ
+ isinφ)3 = (cosφ
+ isinφ)2 • (cosφ
+ isinφ) = (cos2φ + 2icosφsinφ - sin2φ) • (cosφ + isinφ) = cos3φ + icos2φsinφ + 2icos2φsinφ - 2cosφsin2φ - sin2φcosφ - isin3φ = (cos3φ - 2cosφsin2φ - sin2φcosφ) + i • (cos2φsinφ + 2cos2φsinφ - sin3φ) = (cos3φ - 3sin2φcosφ) + i • (3cos2φsinφ - sin3φ) (cosφ + sinφ)3 = cos3φ + isin3φ van die getallen moeten het reële deel en het imaginair deel gelijk zijn, dus moet gelden cos3φ = cos3φ - 3sin2φcosφ en sin3φ = 3cos2φsinφ - sin3φ |
||||
| c. | z1
= 1 • (cosα + isinα) z2 = 1 • (cosβ + isinβ) Dan is z1 • z2 = 1 • (cos(α + β) + i(sin(α + β)) (hoeken optellen) ........(1) Maar ook is z1 • z2 = (cosα + isinα)(cosβ + isinβ) = cosαcosβ + icosαsinβ + isinαcosβ - sinαsinβ = (cosαcosβ - sinαsinβ) + i(cosαsinβ + sinαcosβ) .........(2) De imaginaire delen en de reële delen van (1) en (2) moeten aan elkaar gelijk zijn, en dat geeft direct de gezochte fomules. |
||||
| 10. | a. | Neem z = cosφ
+ isinφ Dan heeft z-1 dezelfde straal maar de hoek tegengesteld, dus z-1 = cos(-φ) + isin(-φ) Dat geeft z-1 = cosφ - isinφ en dat is inderdaad de geconjugeerde (reële deel gelijk, imaginaire deel tegengesteld) |
|||
| b. | z • z-1 = 1 = (cosφ + isinφ)(cosφ - isinφ) = cos2φ + isinφcosφ - icosφsinφ + sin2φ = cos2φ + sin2φ | ||||
|
© h.hofstede (h.hofstede@hogeland.nl) |
|||||