Poolcoördinaten.

© h.hofstede (h.hofstede@hogeland.nl)
Tot nu toe gaven we de plaats van een complex getal in het complexe vlak aan door z = a + bi.  Het getal a heette het reële deel (Rez) van z en b heette het imaginaire deel (Imz)
Dat werkte uitstekend, immers elk punt in een vlak is weer te geven door twee coördinaten.
Maar er is nog een andere manier om de plaats van een punt in een plat vlak weer te geven.
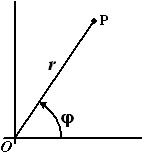
En dat is door zogenaamde "poolcoördinaten". Hiernaast zie je hoe dat in zijn werk gaat.
Als je van een punt P aangeeft hoe groot zijn afstand tot de oorsprong (r) is, en bovendien over welke hoek OP vanaf de positieve horizontale as is gedraaid (φ) dan ligt de plaats van P vast.
In plaats van P aan te geven met  (x, y) of  (Rez, Imz) is het ook mogelijk P te geven met de twee getallen (r, φ). Deze twee "coördinaten" heten poolcoördinaten.

Het verband tussen de coördinaten (a, b)  van  z = a + bi  en deze nieuwe poolcoördinaten zie je in de figuur hieronder.

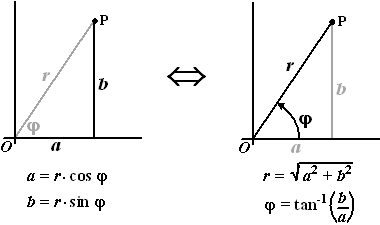
De omrekeningen onder de figuren zijn uiteraard gevonden door Pythagoras en sos-cas-toa te gebruiken, maar dat had je natuurlijk al meteen door....
Een  paar puntjes om op te letten wat betreft die hoek  φ:
• De oorsprong werd in het "oude" systeem gegeven door  0 + 0i.  Maar met poolcoördinaten kun je voor φ eigenlijk alles nemen, zolang r maar 0 is bevind je je altijd in de oorsprong.
• Geef altijd duidelijk aan of je hoeken in graden of radialen meet!
• Die φ is niet éénduidig bepaald. Als je in een punt P kunt komen met een hoek φ = 40º, dan is ook een hoek  400º goed, of  760º of  -320º of......
• De punten  z = -2 + 3i  en   z = 3 - 2i  geven nu dezelfde r en φ.  Ai.....
De functie tan-1 geeft altijd een hoek tussen  -1/2π en 1/2π. Dat betekent dat we hoeken in het tweede en derde kwadrant nooit kunnen krijgen!
Er zijn twee mogelijke oplossingen voor dit "probleem":
oplossing 1: 
Maak je niet zo druk!
Gewoon steeds even opletten of de hoek wel in het juiste kwadrant uitkomt, en als dat niet zo is, er 180º (of π rad natuurlijk)  bij optellen.
oplossing 2:
Spreek nauwkeuriger af hoe φ afhangt van a en b.
Je zou dan zoiets moeten afspreken:
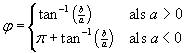
Voorlopig kies ik voor oplossing 1. Jij ook???
Nog een paar namen.

De grootte van r die bij een complex getal hoort (dus in feite de afstand in het complexe vlak van het getal tot de oorsprong) heet ook wel de modulus van dat getal, of ook wel de absolute waarde ervan (voor reële getallen is het inderdaad de absolute waarde zoals we die gewend zijn). De modulus wordt genoteerd met absolute waarde strepen, dus als | z |.

De hoek j  heet ook wel het argument van een complex getal. Je noteert het als arg(z).
Als de j noemt die tussen -180c en 180º ligt, dan spreken we ook wel van de hoofdwaarde van het argument van z, en noteer je het met een hoofdletter:  Arg(z) 

Samengevat:
z  =  a + bi  =  r · (cosj + i · sinφ)
•   r = | z | = Ö(a2 + b2)  en    φ = arg(z) = tan-1(b/a)
•   a = r · cosφ    en    b = r · sinφ
   
Waarom al die moeite?

Nou,  ik hoop dat je je nog kunt herinneren dat een vermenigvuldiging met  i  een paar lessen geleden ooit is ingevoerd in het complexe vlak als een draaiing over 90º . Daarom kun je je misschien wel voorstellen dat vermenigvuldigen van complexe getallen best veel te maken zal hebben met draaiingen. En draaiingen laten zich nou eenmaal erg makkelijk met poolcoördinaten beschrijven, want daar staat al een hoek in.

Alvast als vooruitblik op de komende lessen:
Bij vermenigvuldigen (en delen) van complexe getallen is het vaak handig gebruik te maken van poolcoördinaten. Bij optellen (en aftrekken) van complexe getallen zullen we vaak gebruik maken van "gewone" coördinaten.
   
   

   

het complexe vlak

    

draaivermenigvuldigen
   
  OPGAVEN
1. Schrijf de volgende complexe getallen met poolcoördinaten. Geef de hoeken in graden en rond alles (indien nodig) af op twee decimalen.
a. 3 + 4i

5 en 53,13
g. -3 - 4i

5 en -126,87
b. -2 + 3i

3,61 en 123,69
h. 1,5 - 1,5i

2,12 en -45
c. 1 - i

Ö2 en -45
i. √3 + i

2 en 30
d. 2,8 + 5,2i

5,91 en 61,70
j. √2 - i√2

2 en -45
  e. 8

8 en 0
k. -8 + 12i

 Ö208 en 123,69
  f. 4i

4 en 90
l. 3sin(10º) + 3icos(10º)

3 en 80
2. Schrijf de volgende complexe getallen als a + bi. De hoeken zijn in graden. Rond, indien nodig, a en b af op twee decimalen.
             
a. 2(cos40º + isin40º)

1,53  + 1,29i
f. 5 + isin420º - 2i - 2

3 - 1,13i
b. cos120º + isin120º

-0,5 + 0,5iÖ3
g. 4(cos60º + isin45º)

2 + 2i√2
c. 4isin30º + 4cos30º

2Ö3 +  2i
h. -2 + isin80º

-2 + 0,98i
  d. -2(cos10º - isin10º)

-1,97 + 0,35i
i. i(sin50º + icos50º)

-0,64 + 0,77i
  e. cos(90º) + 3isin(90º)

 3i
       
3. Teken in het complexe vlak de getallen z waarvoor geldt:  (j is in radialen)
           
a. r > 3
b. 0 ≤ φ ≤ 1/2π
c. 2 < | z | < 4
d. 3/4π < arg(z) < π  en  | z | ≤ 2
e. φ = π  en  r > 3
f. φ = r  met  φ ≥ 0
4. Als z = z1 + z2  dan geldt in het algemeen niet dat  | z | = | z1 | + | z2 |
Leg met een tekening uit in welke speciale gevallen deze laatste regel wél geldt.
   
5.
  Waarbij die laatste de geconjugeerde van z was, dat wist je hopelijk nog wel....
 

© h.hofstede (h.hofstede@hogeland.nl)